4 Tema 4: Distribuciones Discretas
4.1 Bernoulli
Sea \(X\) una v.a, se dice que \(X\sim Bernoulli(p)\) si su función de probabilidad es:
\[p(x)=P(X=x)= p^x (1-p)^{1-x} \hspace{0.5cm}; x=\{0,1\}\]
Probabilidad de éxito:
\[P(X=1)=p^1(1-p)^{1-1}=p\]
Probabilidad de fracaso:
\[P(X=0)=p^0(1-p)^{1-0}=1-p\]
Ejemplo 1, Sea el experimento lanzar una moneda y la variable aleatoria \(X\), sale cara \(X=1\), \(X=0\) cuando no salga cara, si suponemos que la moneda es legal, \(p=0.5\). \(X\sim Bernoulli(p=0.5)\)
Ejemplo 2, Sea el experimento lanzar dos dados y sumar el resultados de las caras, si definimos la variable aleatoria como \(X=1\) cuando la suma es 12 y \(X=0\) en otro caso, si asumimos que los dos dados son legales, en este caso el valor de \(p=1/36\), \(X\sim Bernoulli(p=1/36)\)
Ejemplo 3, En el juego del cacho la mejor jugada es cuando todos los dados tienen el mismo número, normalmente se juega con 5 dados. (1,1,1,1,1), (2,2,2,2,2), …, (6,6,6,6,6). Modele la variable aleatoria y defina la distribución. Sea \(X\) la va, \(X=1\) cuando todos los dados son iguales y \(X=0\) en otro caso. Si suponemos que los dados son legales, el valor de \(p=\frac{6}{7776}=\frac{3}{3888}=\frac{1}{1296}\), \(X\sim Bernoulli(p=1/1296)\)
Donde;
\[E[x]=p\]
Demostración:
\[E(X)=\sum_{Rx}xP(X=x)= 0*(1-p)+1*p=p\]
\[V[x]=p*(1-p)\]
\[E[X^2]=\sum_{Rx}x^2P(X=x)=0^2 (1-p)+1^2p=p\]
\[V(X)=E[X^2]-E[X]^2=p-p^2=p(1-p)\]
4.1.1 Usos Bernoulli
\(X\) representa éxito (\(X=1\)) o fracaso (\(X=0\)) en la realización de un proceso al azar. Con \(p\) la probabilidad de éxito \(0<p<1\).
4.2 Binomial
Sea \(X\) una v.a, se dice que \(X\sim Binomial(n,p)\) si su función de probabilidad es: \[p(x)=P(X=x)= {n \choose x} p^x (1-p)^{n-x} \hspace{0.5cm}; x=\{0,1,\ldots,n\}\] Donde;
\[\begin{array}{ll} E[x] & =n*p\\ V[x] & =n*p*(1-p)\\ M_X(t) & =(p*e^t+(1-p))^n \end{array} \] Demostración,
Sea \(X_1, X_2,\ldots,X_n\) \(n\) variables aleatorias independientes entre ellas e idénticamente distribuidas, \(X_i \sim Bernoulli(p)\) para todo \(i=1, \ldots, n\). Sea \(X\) una variable aleatoria, tal que \(X=X_1+X_2+\ldots+X_n\), se dice que \(X \sim Binomial(n,p)\), en ese sentido:
\[E[X]=E[X_1+X_2+\ldots+X_n]=E[X_1]+\ldots+E[X_n]=p+p+\ldots+p=np\] Nota 1. Si tengo dos variables \(X\) e \(Y\) y estas son independientes, entonces:
\[V(X+Y)=V(X)+V(Y)\]
Caso contrario, si no son independientes
\[V(X+Y)=V(X)+V(Y)+2*COV(X,Y)\]
\[V(X)=V(X_1+X_2+\ldots+X_n)=V(X_1)+V(X_2)+\ldots+V(X_n)=p*(1-p)+p(1-p)+\ldots+p(1-p)\] \[V(X)=np(1-p)\]
4.2.1 Usos Binomial
\(X\) representa el número de éxitos en \(n\) ensayos independientes Bernoullis. Con \(p\) la probabilidad de éxito \(0<p<1\) en un ensayo bernoulli.
4.2.2 Ejemplos
- Un estudiante rinde un examen con 10 preguntas de opción múltiple, donde cada pregunta contiene hasta 5 alternativas de respuesta, donde solo una es correcta. Si el estudiante responde las preguntas al azar, defina la distribución de probabilidad que modela el problema y calcula la probabilidad que el estudiante;
- Conteste todas las preguntas de forma incorrecta
- Conteste todas las preguntas de forma correcta
- Obtenga más de la mitad de las respuestas correctas
Respuesta,
El experimento Bernoulli es responder una pregunta al azar con probabilidad de exito de \(p=1/5\)
\(X\): El número de preguntas respondidas de forma correcta, \(X\sim Binomial(n=10,p=1/5)\)
\[P(X=x)= {10 \choose x} 0.2^x 0.8^{10-x} \hspace{0.5cm}; x=\{0,1,\ldots,10\}\]
\[P(X=0)={n \choose x} p^x (1-p)^{n-x}={10 \choose 0} 0.2^0 (1-0.2)^{10-0}=0.107\]
\[P(X=10)={n \choose x} p^x (1-p)^{n-x}={10 \choose 10} 0.2^{10} (1-0.2)^{10-10}=0.0000001024\]
\[P(X>5)=P(X=6)+P(X=7)+P(X=8)+P(X=9)+P(X=10)=\sum_{x=6}^{10}{P(X=x)}=0.0064\] d) ¿Cuál es la probabilidad que el estudiante responde entre 4 a 6 preguntas de forma correcta?
\[P(4\leq X \leq 6)=P(X=4)+P(X=5)+P(X=6)={10 \choose 4} 0.2^4 0.8^{10-4}+{10 \choose 5} 0.2^5 0.8^{10-5}+{10 \choose 6} 0.2^6 0.8^{10-6}\]
\[P(4\leq X \leq 6)=0.088+0.026+0.005=0.119\]
La \(E[X]=np=10*0.2=2\), \(V(X)=np(1-p)=npq=10*0.2*0.8=1.6\), \(\sqrt{V(X)}=\sqrt{1.6}=1.26\)
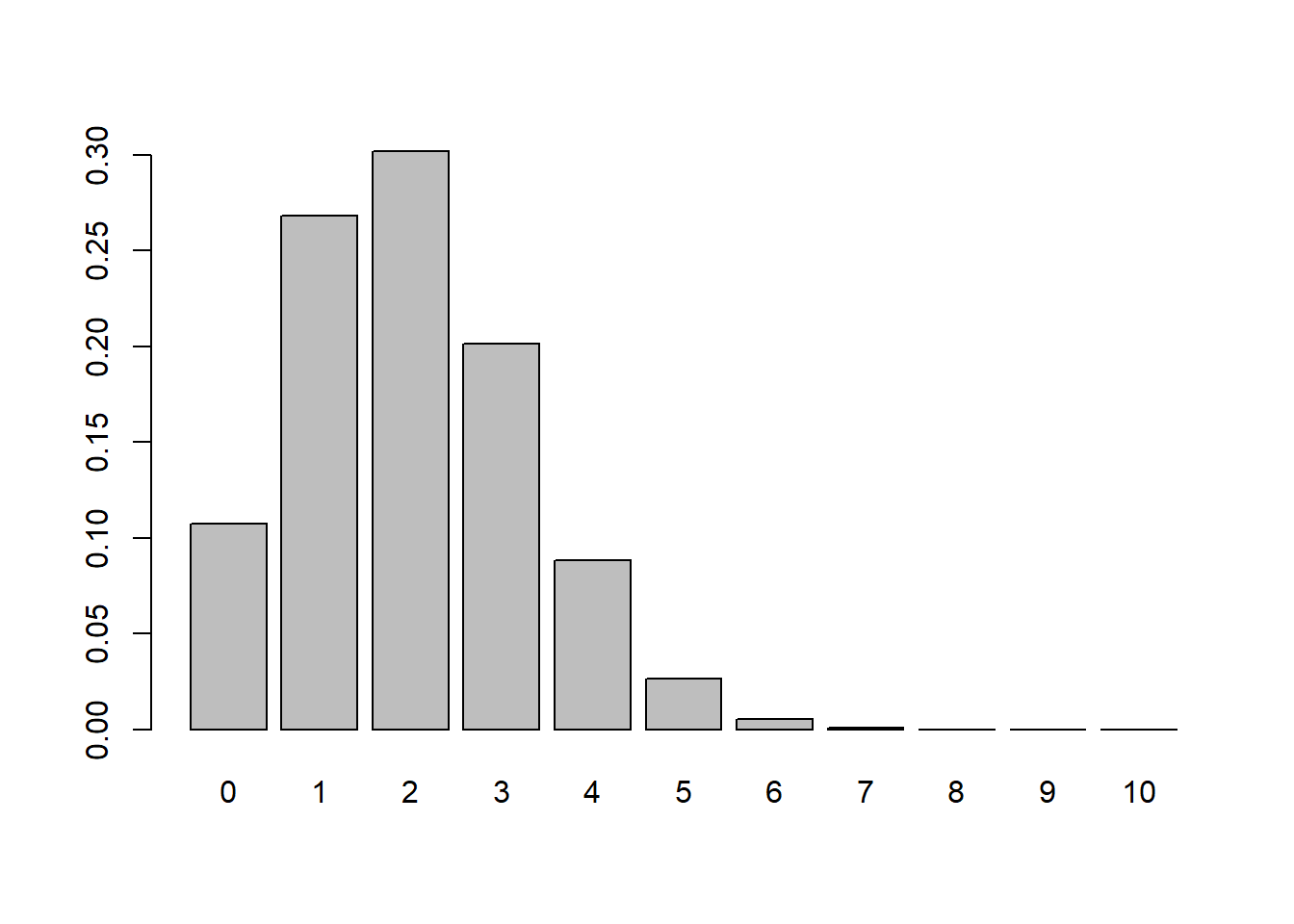 Nota: Sea \(X_1,X_2,\ldots,X_n\), donde \(X_i \sim Bernoulli(p)\) para todo \(i=1:n\), si definimos a \(Y=X_1+X_2+\ldots+X_n\), \(Y\sim Binomial(n,p)\).
Nota: Sea \(X_1,X_2,\ldots,X_n\), donde \(X_i \sim Bernoulli(p)\) para todo \(i=1:n\), si definimos a \(Y=X_1+X_2+\ldots+X_n\), \(Y\sim Binomial(n,p)\).
\[E[Y]=E[X_1+X_2+\ldots+X_n]=E[X_1]+E[X_2]+\ldots+E[X_n]=p+p+\ldots+p=np\]
Ejercicio, Supongamos que un jugador de basketball tiene una probabilidad de 7/9 de encestar un tiro libro y sus tiros son independientes. Si el consigue 5 tiros libres en un juego en particular. ¿Cuál es la probabilidad de que él enceste 2 o más tiros?.
Solución:
X: Número de tiros correctos, \(X\sim Binomial(n=5,p=7/9)\), \(Rx=\{0,1,2,3,4,5\}\)
\[P(X\geq 2)=\sum_{x=2}^{x=5}{P(X=x)}=P(X=2)+P(X=3)+P(X=4)+P(X=5)\]
\[P(X\geq 2)=1-P(X<2)=1-[P(X=0)+P(X=1)]=1- \left( {5 \choose 0} (7/9)^0 (1-7/9)^{5-0}+{5 \choose 1} (7/9)^1 (1-7/9)^{5-1} \right)\]
\[P(X\geq2)=1-(0.00054+0.00948)=0.98997\]
4.3 Geométrica
Sea \(X\) una v.a, se dice que \(X\sim G(p)\) si su función de probabilidad es: \[p(x)=P(X=x)= p (1-p)^{x} \hspace{0.5cm}; x=\{0,1,\ldots\}\]
Donde; \[\begin{array}{ll} E[x] & =\frac{(1-p)}{p}\\ V[x] & =\frac{(1-p)}{p^2}\\ M_X(t) & = \frac{p}{1-(1-p)*e^t} \hspace{0.5cm} \end{array} \]
Miremos algunas probabilidades,
\[P(X=0)=p(1-p)^0=p\] \[P(X=1)=p(1-p)^1\] \[P(X=2)=p(1-p)^2\] \[P(X=2)=P(F_1 \cap F_2 \cap E_3)=P(F_1)*P(F_2)*P(E_1)=(1-p)*(1-p)*p=(1-p)^2p\] Tarea,
Demostrar que la distribución geométrica es una distribución de probabilidad.
\[\sum_{Rx} P(X=x)=1 \] \[\sum_{x=0}^\infty p (1-p)^x=\frac{p}{1-(1-p)}=1\] Resolver,
\[F(t)=P(X\leq t)=\sum_{x=0}^t p (1-p)^x\]
4.3.1 Usos Geométrica
\(X\) representa el número de fracasos antes de obtener el primer éxito en ensayos sucesivos Bernoullis. Con \(p\) la probabilidad de éxito \(0<p<1\).
4.3.2 Ejemplos
- Se realiza el lanzamiento de una moneda legal, Sea X una va, donde X: El número de fracasos antes de sacar Cara por primera vez. Calcular la probabilidad de \(X=10\), \(X=0\), \(X=5\).
Solución, \(X\sim G(p=0.5)\).
- \(P(X=10)=p (1-p)^x=0.5*0.5^{10}=0.00049\)
- \(P(X=0)=p (1-p)^x=0.5*0.5^0=0.5\)
- \(P(X=5)=0.5*0.5^5=0.0156=P(S_1\cap S_2\cap S_3\cap S_4 \cap S_5 \cap C_6)=P(S)^5*P(C)\)
- Una persona se compra un boleto de lotería cada mes, se conoce que en cada sorteo participan 100,000 boletos de lotería, 1) modele el problema, 2) calcule la probabilidad que esta persona gane la lotería el primer mes, 3) la probabilidad que gane la lotería en el mes 13, 4) La probabilidad que gane la lotería el primer año. 5) ¿Cuántos meses se espera hasta que esta persona gane la lotería?
Solución,
- X: El número de meses antes de ganar la lotería, \(X\sim G(p=1/100000)\)
- \(P(X=0)=p(1-p)^x=p(1-p)^0=p=\frac{1}{100000}\)
- \(P(X=12)=p(1-p)^{12}=1/100000*(1-1/100000)^{12}=0.000009998\)
- \(P(X=0)+P(X=1)+P(X=2)+\ldots+P(X=11)=P(X<12)=P(X\leq11)=TAREA\)
- \(E[X]=\frac{(1-p)}{p}=\frac{1-1/100000}{1/100000}=99999\), \(V(X)=\frac{1-p}{p^2}=9999900000\), \(\sqrt{V(x)}=99999.5\)
Imaginemos que la persona compra 15 boletos de lotería cada mes, con este cambio, en cuantos años se espera que la persona pueda ganar la lotería. (TAREA)
4.4 Binomial Negativa
Sea \(X\) una v.a, se dice que \(X\sim BN(r,p)\) si su función de probabilidad es: \[p(x)=P(X=x)= {r+x-1 \choose x} p^r (1-p)^{x} \hspace{0.5cm}; x=\{0,1,\ldots\}\] Donde;
\[\begin{array}{ll} E[x] & =\frac{r*(1-p)}{p}\\ V[x] & =\frac{r*(1-p)}{p^2}\\ M_X(t) & = \left(\frac{p}{1-(1-p)*e^t} \right)^r \hspace{0.5cm} ;t<ln(1/(1-p)) \end{array} \]
4.4.1 Usos Binomial Negativa
\(X\) representa el número de fracasos antes de obtener \(r\) éxitos en ensayos sucesivos Bernoullis. Con \(p\) la probabilidad de éxito \(0<p<1\).
4.4.2 Ejemplo,
- (pg 471, 3). Una moneda correcta es lanzada sucesivamente hasta que aparezca cara por décima vez. Sea X la va que denota el número de sellos que ocurren. Hallar la función de probabilidad de \(X\).
Solución, \(X\sim BN(r=10,p=0.5)\)
\[P(X=x)= {9+x \choose x} 0.5^{10} 0.5^x \]
- Supongamos que una sucesión de lanzamientos independientes es hecho con una moneda, cuya probabilidad de obtener cara en cualquiera de los lanzamientos es de \(1/30\)
- ¿Cuál es la esperanza del número de sellos que se pueden obtener antes de que se obtengan 5 caras?
- ¿Cuál es la varianza del número de sellos que se pueden obtener antes de que se obtengan 5 caras?
Solución, \(X\sim BN(r=5,p=1/30)\), X: El número de sellos antes de obtener 5 caras
- \(E[X]=\frac{r*(1-p)}{p}=\frac{5*(29/30)}{1/30}=145\)
- \(V(X)=\frac{r*(1-p)}{p^2}=\frac{5*(29/30)}{(1/30)^2}=4350\), \(\sqrt{V(X)}=65\)
Tarea 1,
Tres personas tiran monedas al aire y el disparejo paga el café. Si los tres resultados son iguales, las monedas se tiran nuevamente. Encuentre la probabilidad de que se necesitan menos de 4 intentos. (Pg: 476, 30)
Nota: BN(r=1, p) = G(p)
Tarea 2,
Para la distribución geométrica, demostrar:
\[E[X]=\frac{(1-p)}{p}\]
\[E[X]=\sum_{Rx}{x*P(X=x)}=\sum_0^{\infty}{xp(1-p)^x}=\frac{(1-p)}{p}\]
4.5 Hipergeométrica
Sea \(X\) una v.a, se dice que \(X\sim H(N,n,r)\) si su función de probabilidad es: \[p(x)=P(X=x)= \frac{{N-r \choose n-x}{r \choose x}}{{N \choose n}} \hspace{0.5cm}; max\{0,n-N+r\} \leq x \leq min\{r,n\}\] Donde;
\[\begin{array}{ll} E[x] & =n*\frac{r}{N}\\ V[x] & =n * \frac{r}{N} * \frac{N-r}{N} * \frac{N-n}{N-1}\\ \end{array} \]
4.5.1 Usos Hipergeométrica
\(X\) denota el número de elementos que poseen la característica \(A\) en una muestra aleatoria de tamaño \(n\) seleccionado de una población de \(N\) elementos de los cuales \(r\) tienen característica \(A\) y \(N-r\) característica \(B\).
4.5.2 Ejemplo
- En una urna con 30 bolas de colores (10 negras, 5 blancas, 15 verdes). Se seleccionan 7 bolas de forma aleatoria y sin reposición. Si el interés es calcular la probabilidad de obtener bolas negras:
- Modelar la distribución que se ajusta al problema
- Calcular la probabilidad que se seleccionen; 0 bolas negras, todas negras, al menos 2 bolas negras.
Solución, \(X\sim H(N=30,n=7,r=10)\), \(max(0,7-30+10) \leq x \leq min(10,7)\), \(0 \leq x \leq 7\)
\[P(X=0)=\frac{{20 \choose 7-x}{10 \choose x}}{{30 \choose 7}}=\frac{{20 \choose 7}{10 \choose 0}}{{30 \choose 7}}=\frac{77520*1}{2035800}=\frac{77520}{2035800}=0.038\] \[P(X=7)==\frac{{20 \choose 0}{10 \choose 7}}{{30 \choose 7}}=\frac{120}{2035800}=0.000059\]
\[P(X\geq 2)=P(X=2)+P(X=3)+...+P(X=7)\] \[P(X\geq 2)=1-P(X<2)=1-[P(X=0)+P(X=1)]=1-0.038-\frac{{20 \choose 6}{10 \choose 1}}{{30 \choose 7}}=1-0.038-0.19=0.772\]
¿Cuál es la probabilidad de obtener 3 negras, 3 verdes y una blanca?
\[P(3N \cap 3V \cap 1B)=\frac{{10 \choose 3}{15 \choose 3}{5 \choose 1}}{{30 \choose 7}}\]
Tarea (Pg 459, Ej 8)
4.6 Poisson
Sea \(X\) una v.a, se dice que \(X\sim P(\lambda)\), (\(\lambda>0\)) si su función de probabilidad es: \[p(x)=P(X=x)= \frac{e^{-\lambda} \lambda^x}{x!} \hspace{0.5cm}; x=\{0,1,2, \ldots \}\] Donde;
\[\begin{array}{ll} E[x] & =\lambda\\ V[x] & =\lambda\\ M_X(t) & =e^{\lambda (e^t -1)} \end{array} \]
4.6.1 Usos Poisson
\(X\) representa el número de eventos de cierto tipo, que ocurren en un intervalo de tiempo, o en una región, o en un volumen.
- Fallas de un computador en un día de operación
- Número de clientes que entran a un banco en un día dado
Nota: Si \(X \sim binomial(n,p)\), si \(n \rightarrow \infty\) , \(p \rightarrow 0\) y \(\lambda=n*p\) permanece constante. Entonces se puede aproximar con \(X \sim Poisson(\lambda = n*p)\). \(n \geq 50\), \(p\leq 0.1\).
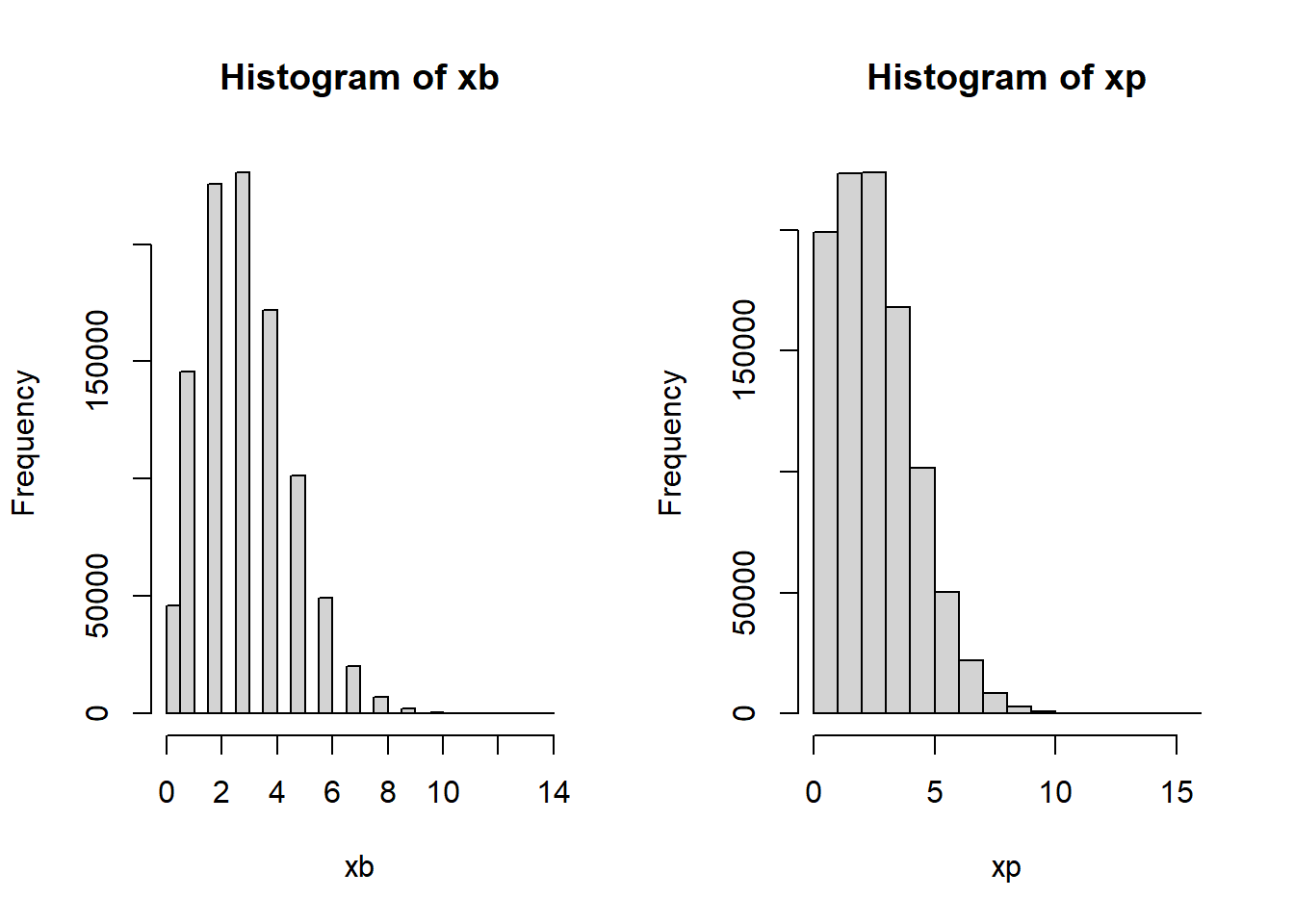
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 2.000 3.000 3.001 4.000 14.000## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 2.000 3.000 3.002 4.000 16.000Ejercicios,
- Verificar si efectivamente la distribución de Poisson es una distribución de probabilidad.
\[1=\sum_{Rx} P(X=x)=\sum_{x=0}^\infty {\frac{e^{-\lambda} \lambda^x}{x!}}=e^{-\lambda}\sum_{x=0}^\infty {\frac{\lambda^x}{x!}}= e^{-\lambda} e^\lambda =e^0=1 \] Esto recordando que:
\[e^y=\sum_{x=0}^\infty {\frac{y^x}{x!}}\] 2. Demostrar que si \(X\sim P(\lambda)\) la \(E[X]=\lambda\),
\[\lambda=E[X]=\sum_{Rx}x P(X=x)=\sum_{x=0}^\infty {\frac{x e^{-\lambda} \lambda^x}{x!}}=e^{-\lambda}\lambda \sum_{x=0}^\infty {\frac{x \lambda^x}{x! \lambda}}=e^{-\lambda}\lambda \sum_{x=0}^\infty {\frac{x \lambda^{x-1}}{x! }}=\] \[=e^{-\lambda}\lambda \sum_{x=1}^\infty {\frac{x \lambda^{x-1}}{x (x-1)! }}=e^{-\lambda}\lambda \sum_{x-1=0}^\infty {\frac{ \lambda^{x-1}}{(x-1)! }}=e^{-\lambda}\lambda \sum_{y=0}^\infty {\frac{ \lambda^{y}}{y! }}=\lambda e^{-\lambda}e^\lambda=\lambda\]
4.6.2 Ejemplos
- Cierta oficina de bomberos recibe en promedio 3 llamadas por día, calcular la probabilidad de que:
- Reciba 4 llamadas en un día
Solución, X: Número de llamadas que recibe la oficina de bomberos en un día, tener en cuenta que el promedio o la media puede ser tomada como un sinónimo de la esperanza matemática \(E[X]\). Así, la información dada es \(E[X]=3=\lambda\), entonces, \(X\sim P(\lambda=3)\)
\[P(X=4)=\frac{e^{-\lambda} \lambda^x}{x!}=\frac{e^{-3}3^4}{4!}=\frac{4.0327}{24}=0.168\]
- Reciba 3 o más llamadas en un día
Solución, \(X\sim P(\lambda=3)\)
\[P(X\geq 3)=1-P(X<3)=1-[P(X=0)+P(X=1)+P(X=2)]=\ldots\]
- Reciba 10 llamadas en una semana (7 días)
Solución, X: el número de llamadas a la oficina de bomberos durante 7 días. La idea es aplicar una regla de tres para re escalar la información, sabemos que en promedio se reciben 3 llamadas por día, en 7 días se espera en promedio que se reciban \(3*7=21=E[X]=\lambda\). Entonces, \(X\sim P(\lambda=3*7=21)\)
\[P(X=10)=\frac{e^{-21}21^{10}}{10!}=0.00348\]
- ¿Cuántas llamadas en promedio se espera tener durante un año (365 días)?
Solución: 3*365=1095
- Suponga que hay en promedio 2 suicidios por año en una población de 50 mil habitantes. En una ciudad de 100 mil habitantes. Encuentre la probabilidad de que en un año dado haya:
- Un suicidio
- 2 o más suicidios
Solución, X: Número de suicidios por año en ciudad de 100 mil habitantes, \(X\sim P(\lambda=4)\).
\[P(X=1)=\frac{e^{-4}4^1}{1!}=0.0733\] \[P(X\geq 2)=1-P(X<2)=1-[P(X=0)+P(X=1)]=1-\frac{e^{-4}4^0}{0!}-\frac{e^{-4}4^1}{1!}=0.908\]
#######################################3
\[P(X=8)= \frac{{100 \choose 2}{30 \choose 8}}{{130 \choose 10}} \hspace{0.5cm}\]