1 Minería de Datos

1.1 Motivación para la Minería de datos

(Variedad) Los métodos de recolección de datos han evolucionado muy rápidamente.
(Volumen) Las bases de datos han crecido exponencialmente
(Usuarios) Estos datos contienen información útil para las empresas, países, etc.
(Tecnología) El tamaño hace que la inspección manual sea casi imposible
(Método) Se requieren métodos de análisis de datos automáticos para optimizar el uso de estos enormes conjuntos de datos

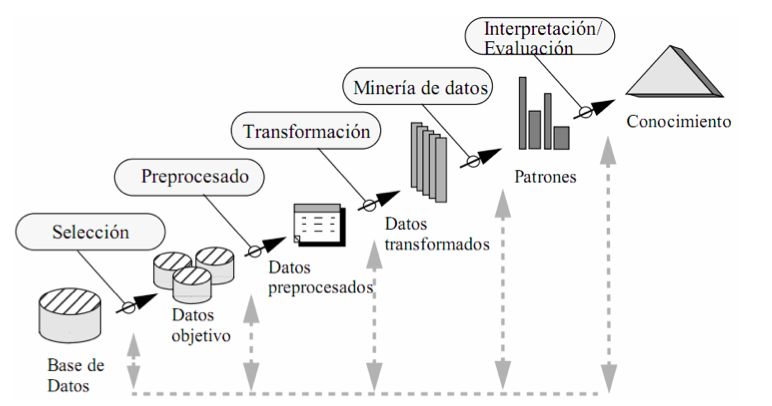
1.2 ¿Qué es la minería de datos?

Es el análisis de conjuntos de datos (a menudo grandes) para encontrar relaciones insospechadas (conocimiento) y resumir los datos de formas novedosas que sean comprensibles y útiles para el propietario/usuario de los datos.

Principles of Data Mining (Hand et.al. 2001)

1.3 Datos y conocimiento (Insumo/Resultado)

1.3.1 Datos:

se refieren a instancias únicas y primitivas (single objetos, personas, eventos, puntos en el tiempo, etc.)
describir propiedades individuales
a menudo son fáciles de recolectar u obtener (por ejemplo, cajeros de escáner, internet, etc.)
no nos permiten hacer predicciones o pronósticos

Ejercicio:

Elija un sector/área y describa los potenciales datos que se tienen disponibles

1. Salud (Hospital): Registros de pacientes, medicamentos, vacunas, fichas epidemiológicas, personal médico, consultorios (infraestructura), financiera
1. (Seguridad) Feminicidios: Casos, lugar, entorno familiar, denuncias previas, sospechosos, información forense, Caracterizar al culpable
1. Banca: Prestamos; ingresos, laboral. Caja de ahorro; personal, movimientos. Cajas; Servicios, etc. Cajeros; Lugar, movimientos. Clientes; Prestamistas; Deuda, mora, juicio, ahorristas. Base de datos de patrimonio
1. Geografía: Clima; Lluvia, Minas; tipo, trabajadores, cultivos; tipo, temporada, tipo suelo, montañas, pluvial, temperatura.

1.3.2 Conocimiento:

(Características) se refiere a clases de instancias (conjuntos de …)
(Forma) describe patrones generales, estructuras, leyes,
(Declaración) consta de la menor cantidad de declaraciones posibles
(Proceso) a menudo es difícil y lleva mucho tiempo encontrar u obtener
(Acciones) nos permite hacer predicciones y pronósticos

Ejercicio:

Agrupar la tipología de los pacientes; Mejorar servicio, acciones
Determinantes del feminicidio; SLIM, medidas
Relación el monto del ingreso con el motivo de préstamo; Realizar ofertas, promocionar a clientes.
Relación entre el clima y los cultivos, dado el tipo de mineral se puede pensar en un mercado posterior

1.4 Requerimientos

Disponibilidad para aprender
Mucha paciencia
- Interactúa con otras áreas
- Preprocesamiento de datos
Creatividad
Rigor, prueba y error

1.5 knowledge discovery in databases (KDD)

1.6 Preparación de los datos

1.6.1 Recopilación

Instituto de Estadística
UDAPE, ASFI
Ministerio Salud (SNIS), Ministerio de educación (SIE)
APIs, Twitter, Facebook, etc.
Kaggle
Banco Mundial, UNICEF, FAO, BID (Open Data)

1.6.2 Data Warehouse

1.6.3 Data Warehouse in R

1.6.4 Importación

library(foreign)
library(readr)
apropos("read")
getwd()
setwd("C:\\Users\\ALVARO\\Downloads\\bd49 (1)\\Base EH2019")
dir()
eh19v<-read.spss("EH2019_Vivienda.sav",to.data.frame = T)
eh19p<-read.spss("EH2019_Persona.sav",to.data.frame = T)
object.size(eh19p)/10^6
#exportación de datos
setwd("C:\\Users\\ALVARO\\Documents\\GitHub\\EST-384\\data")
save(eh19p,eh19v,file="eh19.RData")
# cargando la base de datos que acabamos de guardar
rm(list=ls())
load("eh19.RData")
load("oct20.RData")
# cargando desde github
rm(list=ls())
load(url("https://github.com/AlvaroLimber/EST-384/raw/master/data/eh19.RData"))
load(url("https://github.com/AlvaroLimber/EST-384/raw/master/data/oct20.RData"))

1.6.5 Recopilación

read.table("clipboard",header = T)
library(readxl) # excel 
library(DBI)  # Bases de datos relacionales en el sistema
#library(help=DBI)  
library(RMySQL) # bases de datos en mysql
# web scraping (API)
library(gtrendsR) # API
gg<-gtrends(c("data mining","machine learning"),time="today 12-m")
gg$interest_over_time
plot(gg)
gg<-gtrends(c("data mining","machine learning"),time="today 12-m",geo="BO")

1.6.6 Limpieza

std<-data.frame(name=c("ana","juan","carla"),math=c(86,43,80),stat=c(90,75,82))
std

##    name math stat
## 1   ana   86   90
## 2  juan   43   75
## 3 carla   80   82

library(tidyr)
bd<-gather(std,materia,nota,math:stat)
bd

##    name materia nota
## 1   ana    math   86
## 2  juan    math   43
## 3 carla    math   80
## 4   ana    stat   90
## 5  juan    stat   75
## 6 carla    stat   82

# otra opción más relacionada a bases de datos con información de tiempo, 
# es el comando reshape

1.6.7 Ejercicio (reshape)

http://www.udape.gob.bo/portales_html/dossierweb2019/htms/CAP07/C070311.xls

1.6.8 Limpieza (fechas)

library(lubridate)
date()

## [1] "Mon Aug  1 19:01:37 2022"

today()

## [1] "2022-08-01"

ymd("20151021")

## [1] "2015-10-21"

ymd("2015/11/30")

## [1] "2015-11-30"

myd("11.2012.3")

## [1] "2012-11-03"

dmy_hms("2/12/2013 14:05:01")

## [1] "2013-12-02 14:05:01 UTC"

mdy("120112")

## [1] "2012-12-01"

d1<-dmy("15032020")
class(d1)

## [1] "Date"

#ts()

1.6.9 Limpieza (String)

toupper("hola")

## [1] "HOLA"

tolower("HOLA")

## [1] "hola"

abc<-letters[1:10]
toupper(abc)

##  [1] "A" "B" "C" "D" "E" "F" "G"
##  [8] "H" "I" "J"

tolower("Juan")

## [1] "juan"

# Extraer partes de un texto
substr("hola como estan",1,3)

## [1] "hol"

substr("hola como estan",3,7)

## [1] "la co"

# contar la cantidad de caracteres
nchar("hola")

## [1] 4

nchar(c("hola","chau","LA                         paz"))

## [1]  4  4 30

x<-c("LA-.paz","La Paz", "La pas", "La    paz","lapaz","la 78 paz")

x<-toupper(x)

x<-gsub("PAS","PAZ",x)

library(tm)
x<-removeNumbers(x)
x<-removePunctuation(x)
x<-gsub("LAPAZ","LA PAZ",x)
x<-stripWhitespace(x)

nchar(x)

## [1] 6 6 6 6 6 6

nchar(gsub("  "," ",x))

## [1] 6 6 6 6 6 6

gsub("a","x","hola como estas")

## [1] "holx como estxs"

grepl("a",c("hola","como"))

## [1]  TRUE FALSE

grepl("o",c("hola","como"))

## [1] TRUE TRUE

#otra alternativa
x<-c("LA-.paz","La Paz", "La pas", "La    paz","lapaz","la 78 paz")
x<-toupper(x)
x[grepl("PAZ",x)]<-"LA PAZ"
x<-gsub("PAS","PAZ",x)

# para llevar a ascii
utf8ToInt("la paz")

## [1] 108  97  32 112  97 122

utf8ToInt("@")

## [1] 64

library(stringi)

Ejemplo de web scraping sobre la página https://www.worldometers.info/

library(rvest)
url<-"https://www.worldometers.info/coronavirus/"
covid<-read_html(url)
bdcov<-html_table(covid)
bdnow<-bdcov[[1]]
str(bdnow)

## tibble [246 × 22] (S3: tbl_df/tbl/data.frame)
##  $ #                  : int [1:246] NA NA NA NA NA NA NA NA 1 2 ...
##  $ Country,Other      : chr [1:246] "North America" "Asia" "Europe" "South America" ...
##  $ TotalCases         : chr [1:246] "110,499,104" "170,218,328" "215,684,754" "62,298,715" ...
##  $ NewCases           : chr [1:246] "+17,094" "+323,057" "+67,874" "+30,500" ...
##  $ TotalDeaths        : chr [1:246] "1,504,922" "1,448,481" "1,877,696" "1,316,172" ...
##  $ NewDeaths          : chr [1:246] "+53" "+310" "+420" "+187" ...
##  $ TotalRecovered     : chr [1:246] "103,321,710" "161,814,212" "205,992,353" "59,364,292" ...
##  $ NewRecovered       : chr [1:246] "+48,718" "+309,148" "+466,980" "+22,869" ...
##  $ ActiveCases        : chr [1:246] "5,672,472" "6,955,635" "7,814,705" "1,618,251" ...
##  $ Serious,Critical   : chr [1:246] "9,927" "12,468" "7,988" "10,542" ...
##  $ Tot Cases/1M pop   : chr [1:246] "" "" "" "" ...
##  $ Deaths/1M pop      : chr [1:246] "" "" "" "" ...
##  $ TotalTests         : chr [1:246] "" "" "" "" ...
##  $ Tests/1M pop       : chr [1:246] "" "" "" "" ...
##  $ Population         : chr [1:246] "" "" "" "" ...
##  $ Continent          : chr [1:246] "North America" "Asia" "Europe" "South America" ...
##  $ 1 Caseevery X ppl  : chr [1:246] "" "" "" "" ...
##  $ 1 Deathevery X ppl : chr [1:246] "" "" "" "" ...
##  $ 1 Testevery X ppl  : int [1:246] NA NA NA NA NA NA NA NA NA 2 ...
##  $ New Cases/1M pop   : chr [1:246] "" "" "" "" ...
##  $ New Deaths/1M pop  : num [1:246] NA NA NA NA NA NA NA NA NA NA ...
##  $ Active Cases/1M pop: chr [1:246] "" "" "" "" ...

Tarea: limpiar la base de datos

Convertir las variables necesarias a numéricas
Debe ser una base de solo países

1.6.10 Transformación

load(url("https://github.com/AlvaroLimber/EST-384/raw/master/data/eh19.RData"))
names(eh19p)

##   [1] "folio"         
##   [2] "depto"         
##   [3] "area"          
##   [4] "nro"           
##   [5] "s02a_02"       
##   [6] "s02a_03"       
##   [7] "s02a_04a"      
##   [8] "s02a_04b"      
##   [9] "s02a_04c"      
##  [10] "s02a_05"       
##  [11] "s02a_06a"      
##  [12] "s02a_06b"      
##  [13] "s02a_06c"      
##  [14] "s02a_06d"      
##  [15] "s02a_06e"      
##  [16] "s02a_06_b"     
##  [17] "s02a_07_1"     
##  [18] "s02a_07_2"     
##  [19] "s02a_07_3"     
##  [20] "s02a_08"       
##  [21] "s02a_10"       
##  [22] "s03a_01a"      
##  [23] "s03a_01b"      
##  [24] "s03a_01c"      
##  [25] "s03a_01d"      
##  [26] "s03a_01d2_cod" 
##  [27] "s03a_01e"      
##  [28] "s03a_02"       
##  [29] "s03a_02e"      
##  [30] "s03a_03"       
##  [31] "s03a_03a"      
##  [32] "s03a_04"       
##  [33] "s03a_04npioc"  
##  [34] "s04a_01a"      
##  [35] "s04a_01b"      
##  [36] "s04a_01e"      
##  [37] "s04a_02a"      
##  [38] "s04a_02b"      
##  [39] "s04a_02e"      
##  [40] "s04a_03a"      
##  [41] "s04a_03b"      
##  [42] "s04a_03c"      
##  [43] "s04a_03d"      
##  [44] "s04a_03e"      
##  [45] "s04a_03f"      
##  [46] "s04a_03g"      
##  [47] "s04a_04a"      
##  [48] "s04a_04b"      
##  [49] "s04a_04e"      
##  [50] "S04A_0"        
##  [51] "S04A_1"        
##  [52] "S04A_2"        
##  [53] "s04a_05a"      
##  [54] "s04a_05b"      
##  [55] "s04a_05c"      
##  [56] "s04a_05d"      
##  [57] "s04a_05e"      
##  [58] "s04a_06a"      
##  [59] "s04a_07a"      
##  [60] "s04a_07a_e"    
##  [61] "s04a_06b"      
##  [62] "s04a_07b"      
##  [63] "s04a_07b_e"    
##  [64] "s04a_06c"      
##  [65] "s04a_07c"      
##  [66] "s04a_07c_e"    
##  [67] "s04a_06d"      
##  [68] "s04a_07d"      
##  [69] "s04a_07d_e"    
##  [70] "s04a_06e"      
##  [71] "s04a_07e"      
##  [72] "s04a_07e_e"    
##  [73] "s04a_06f"      
##  [74] "s04a_07f"      
##  [75] "s04a_07f_e"    
##  [76] "s04a_06g"      
##  [77] "s04a_07g"      
##  [78] "s04a_07g_e"    
##  [79] "s04a_08"       
##  [80] "s04a_08a1"     
##  [81] "s04a_08a2"     
##  [82] "s04a_08b"      
##  [83] "s04a_09"       
##  [84] "s04a_09a"      
##  [85] "s04b_11a"      
##  [86] "s04b_11b"      
##  [87] "s04b_12"       
##  [88] "s04b_13"       
##  [89] "s04b_14a"      
##  [90] "s04b_14b"      
##  [91] "s04b_15"       
##  [92] "s04b_15e"      
##  [93] "S04B_9"        
##  [94] "S04B_A"        
##  [95] "S04B_B"        
##  [96] "s04b_16"       
##  [97] "s04b_16e"      
##  [98] "S04B_6"        
##  [99] "S04B_7"        
## [100] "S04B_8"        
## [101] "s04b_17"       
## [102] "s04b_17e"      
## [103] "S04B_3"        
## [104] "S04B_4"        
## [105] "S04B_5"        
## [106] "s04b_18"       
## [107] "s04b_18e"      
## [108] "S04B_0"        
## [109] "S04B_1"        
## [110] "S04B_2"        
## [111] "s04b_19"       
## [112] "s04b_20a1"     
## [113] "s04b_20a2"     
## [114] "s04b_20b"      
## [115] "s04b_21a"      
## [116] "s04b_21b"      
## [117] "s04b_21b2"     
## [118] "s04c_22"       
## [119] "s04c_23"       
## [120] "s04d_24"       
## [121] "s04d_25"       
## [122] "s04d_26"       
## [123] "s04d_27a"      
## [124] "s04d_27b"      
## [125] "s04e_28a"      
## [126] "s04e_28b"      
## [127] "s04e_29a"      
## [128] "s04e_29b"      
## [129] "s04e_30a"      
## [130] "s04e_30b"      
## [131] "s04e_30c_cod"  
## [132] "s04e_31a"      
## [133] "s04e_31b"      
## [134] "s04e_31c"      
## [135] "s04e_31d"      
## [136] "s04e_31e"      
## [137] "s04e_31f"      
## [138] "s04e_31_e"     
## [139] "s04e_32a"      
## [140] "s04e_32b"      
## [141] "s04e_33a"      
## [142] "s04e_33b"      
## [143] "s04_e_34a"     
## [144] "s04f_34"       
## [145] "s04f_35a"      
## [146] "s04f_35b"      
## [147] "s04f_35c"      
## [148] "s04f_35e"      
## [149] "s05a_01"       
## [150] "s05a_01a"      
## [151] "s05a_02a"      
## [152] "s05a_02c"      
## [153] "s05a_03a"      
## [154] "s05a_03c"      
## [155] "s05a_04"       
## [156] "s05a_05"       
## [157] "s05a_05_e"     
## [158] "s05a_06a"      
## [159] "s05a_06c"      
## [160] "s05a_07a"      
## [161] "s05a_07b"      
## [162] "s05a_08"       
## [163] "s05a_09"       
## [164] "s05b_10"       
## [165] "s05b_11"       
## [166] "s05b_11_e"     
## [167] "s05b_11a"      
## [168] "s05c_13a"      
## [169] "s05c_13b"      
## [170] "s05c_13c"      
## [171] "s05c_13d"      
## [172] "s05c_13e"      
## [173] "s05c_13f"      
## [174] "s05c_13g"      
## [175] "s05c_13h"      
## [176] "s05c_13_e"     
## [177] "s05c_14a"      
## [178] "s05c_14b"      
## [179] "s05c_15a"      
## [180] "s05c_15b"      
## [181] "s05d_17"       
## [182] "s05d_18"       
## [183] "s05d_19a"      
## [184] "s05d_19b"      
## [185] "s05d_20a"      
## [186] "s05d_20b"      
## [187] "s05d_21a"      
## [188] "s05d_21b"      
## [189] "s05d_21e"      
## [190] "s05d_22a"      
## [191] "s05d_22b"      
## [192] "s05d_22c"      
## [193] "s05d_22d"      
## [194] "s05d_22e"      
## [195] "s05d_22f"      
## [196] "s05d_22g"      
## [197] "s05d_22h"      
## [198] "s05d_22i"      
## [199] "s05d_22j"      
## [200] "s05d_22k"      
## [201] "s05d_22l"      
## [202] "s05d_22_e"     
## [203] "s06a_01"       
## [204] "s06a_02"       
## [205] "s06a_03"       
## [206] "s06a_04"       
## [207] "s06a_05"       
## [208] "s06a_06aa"     
## [209] "s06a_06ab"     
## [210] "s06a_06ac"     
## [211] "s06a_06e"      
## [212] "s06a_07"       
## [213] "s06a_08a"      
## [214] "s06a_08b"      
## [215] "s06a_09"       
## [216] "s06a_09e"      
## [217] "s06a_10"       
## [218] "s06a_10e"      
## [219] "s06b_11a"      
## [220] "s06b_11a_cod"  
## [221] "s06b_11b"      
## [222] "s06b_12a"      
## [223] "s06b_12a_cod"  
## [224] "s06b_12b"      
## [225] "s06b_13"       
## [226] "s06b_13a"      
## [227] "s06b_13b"      
## [228] "s06b_13c"      
## [229] "s06b_14"       
## [230] "s06b_15aa"     
## [231] "s06b_15ab"     
## [232] "s06b_15ba"     
## [233] "s06b_15bb"     
## [234] "s06b_15ca"     
## [235] "s06b_15cb"     
## [236] "s06b_15da"     
## [237] "s06b_15db"     
## [238] "s06b_17"       
## [239] "s06b_18"       
## [240] "s06b_19a"      
## [241] "s06b_19b"      
## [242] "s06b_20"       
## [243] "s06b_20e"      
## [244] "s06b_21a"      
## [245] "s06b_21b"      
## [246] "s06b_22"       
## [247] "s06b_23aa"     
## [248] "s06b_23ab"     
## [249] "s06c_25a"      
## [250] "s06c_25b"      
## [251] "s06c_26a"      
## [252] "s06c_26b"      
## [253] "s06c_27aa"     
## [254] "s06c_27ab"     
## [255] "s06c_27ba"     
## [256] "s06c_27bb"     
## [257] "s06c_28a"      
## [258] "s06c_28a1"     
## [259] "s06c_28b"      
## [260] "s06c_29a"      
## [261] "s06c_29b"      
## [262] "s06c_30a"      
## [263] "s06c_30a1"     
## [264] "s06c_30a2"     
## [265] "s06c_30b"      
## [266] "s06c_30b1"     
## [267] "s06c_30b2"     
## [268] "s06c_30c"      
## [269] "s06c_30c1"     
## [270] "s06c_30c2"     
## [271] "s06c_30d"      
## [272] "s06c_30d1"     
## [273] "s06c_30d2"     
## [274] "s06c_30e"      
## [275] "s06c_30e1"     
## [276] "s06c_30e2"     
## [277] "s06d_31a"      
## [278] "s06d_31b"      
## [279] "s06d_32aa"     
## [280] "s06d_32ab"     
## [281] "s06d_32ba"     
## [282] "s06d_32bb"     
## [283] "s06d_32ca"     
## [284] "s06d_32cb"     
## [285] "s06d_32da"     
## [286] "s06d_32db"     
## [287] "s06d_32ea"     
## [288] "s06d_32eb"     
## [289] "s06d_32fa"     
## [290] "s06d_32fb"     
## [291] "s06d_32ga"     
## [292] "s06d_32gb"     
## [293] "s06d_32ha"     
## [294] "s06d_32hb"     
## [295] "s06d_33a"      
## [296] "s06d_33b"      
## [297] "s06d_34"       
## [298] "s06e_35a"      
## [299] "s06e_35a_cod"  
## [300] "s06e_35b"      
## [301] "s06e_36"       
## [302] "s06e_37"       
## [303] "s06e_38a"      
## [304] "s06e_38b"      
## [305] "s06e_39"       
## [306] "s06e_40"       
## [307] "s06e_40b"      
## [308] "s06f_42a"      
## [309] "s06f_42b"      
## [310] "s06f_43a"      
## [311] "s06f_43a1"     
## [312] "s06f_43b"      
## [313] "s06f_43b1"     
## [314] "s06f_43c"      
## [315] "s06f_43c1"     
## [316] "s06f_44a"      
## [317] "s06f_44b"      
## [318] "s06f_45aa"     
## [319] "s06f_45ab"     
## [320] "s06f_45ba"     
## [321] "s06f_45bb"     
## [322] "s06f_45ca"     
## [323] "s06f_45cb"     
## [324] "s06f_45da"     
## [325] "s06f_45db"     
## [326] "s06f_45ea"     
## [327] "s06f_45eb"     
## [328] "s06f_45fa"     
## [329] "s06f_45fb"     
## [330] "s06f_45ga"     
## [331] "s06f_45gb"     
## [332] "s06f_45ha"     
## [333] "s06f_45hb"     
## [334] "s06f_46a"      
## [335] "s06f_46b"      
## [336] "s06g_47"       
## [337] "s06g_48"       
## [338] "s06g_49"       
## [339] "s06g_49e"      
## [340] "s06g_50"       
## [341] "s06g_50e"      
## [342] "s06g_51"       
## [343] "s06g_51e"      
## [344] "s06g_52"       
## [345] "s06g_53"       
## [346] "s06g_54"       
## [347] "s06g_55"       
## [348] "s07a_01a"      
## [349] "s07a_01b"      
## [350] "s07a_01c"      
## [351] "s07a_01d"      
## [352] "s07a_01e"      
## [353] "s07a_01e0"     
## [354] "s07a_01e1"     
## [355] "s07a_01e1e"    
## [356] "s07a_01e2"     
## [357] "s07a_01e2e"    
## [358] "s07a_02a"      
## [359] "s07a_02b"      
## [360] "s07a_02c"      
## [361] "s07a_02ce"     
## [362] "s07a_03a"      
## [363] "s07a_03b"      
## [364] "s07a_03c"      
## [365] "s07a_04a"      
## [366] "s07a_04b"      
## [367] "s07a_04c"      
## [368] "s07a_04d"      
## [369] "s07b_05aa"     
## [370] "s07b_05ab"     
## [371] "s07b_05ba"     
## [372] "s07b_05bb"     
## [373] "s07b_05ca"     
## [374] "s07b_05cb"     
## [375] "s07b_05da"     
## [376] "s07b_05db"     
## [377] "s07b_05de"     
## [378] "s07b_05ea"     
## [379] "s07b_05eb"     
## [380] "s07b_05ee"     
## [381] "s07c_06"       
## [382] "s07c_07"       
## [383] "s07c_08a"      
## [384] "s07c_08b"      
## [385] "s07c_08e"      
## [386] "s07c_09"       
## [387] "s07c_09e"      
## [388] "s07c_10"       
## [389] "s08a_01"       
## [390] "s08a_03a"      
## [391] "s08a_03b"      
## [392] "s08a_03c"      
## [393] "s08a_03e"      
## [394] "s08a_04"       
## [395] "s08a_06"       
## [396] "upm"           
## [397] "estrato"       
## [398] "factor"        
## [399] "tipohogar"     
## [400] "cobersalud"    
## [401] "hnv_ult_a"     
## [402] "quienatenparto"
## [403] "dondeatenparto"
## [404] "niv_ed"        
## [405] "niv_ed_g"      
## [406] "cmasi"         
## [407] "educ_prev"     
## [408] "aestudio"      
## [409] "cob_op"        
## [410] "caeb_op"       
## [411] "pet"           
## [412] "ocupado"       
## [413] "cesante"       
## [414] "aspirante"     
## [415] "desocupado"    
## [416] "pea"           
## [417] "temporal"      
## [418] "permanente"    
## [419] "pei"           
## [420] "condact"       
## [421] "phrs"          
## [422] "shrs"          
## [423] "tothrs"        
## [424] "yprilab"       
## [425] "yseclab"       
## [426] "ylab"          
## [427] "ynolab"        
## [428] "yper"          
## [429] "yhog"          
## [430] "yhogpc"        
## [431] "z"             
## [432] "zext"          
## [433] "p0"            
## [434] "p1"            
## [435] "p2"            
## [436] "pext0"         
## [437] "pext1"         
## [438] "pext2"

Estandarizar variables

summary(eh19p$s02a_03) #edad

##    Min. 1st Qu.  Median    Mean 
##    0.00   12.00   26.00   29.69 
## 3rd Qu.    Max. 
##   44.00   98.00

summary(eh19p$tothrs) # total de horas de trabajo semanal

##    Min. 1st Qu.  Median    Mean 
##    1.00   30.00   42.00   42.29 
## 3rd Qu.    Max.    NA's 
##   54.00  112.50   20454

summary(eh19p$ylab)  # ingreso laboral mensual

##    Min. 1st Qu.  Median    Mean 
##      10    1416    2598    3075 
## 3rd Qu.    Max.    NA's 
##    4000   32917   23816

sd(eh19p$s02a_03)

## [1] 21.05689

sd(eh19p$tothrs,na.rm = T)

## [1] 19.33807

sd(eh19p$ylab,na.rm = T)

## [1] 2470.079

x1<-scale(eh19p$s02a_03)
x2<-scale(eh19p$tothrs)
x3<-scale(eh19p$ylab)

sd(x1);sd(x2,na.rm = T);sd(x3,na.rm = T)

## [1] 1

## [1] 1

## [1] 1

par(mfrow=c(2,3))
boxplot(eh19p$s02a_03,ylim=c(0,25000))
boxplot(eh19p$tothrs,ylim=c(0,25000))
boxplot(eh19p$ylab,ylim=c(0,25000))

boxplot(x1,ylim=c(-3,3))
boxplot(x2,ylim=c(-3,3))
boxplot(x3,ylim=c(-3,3))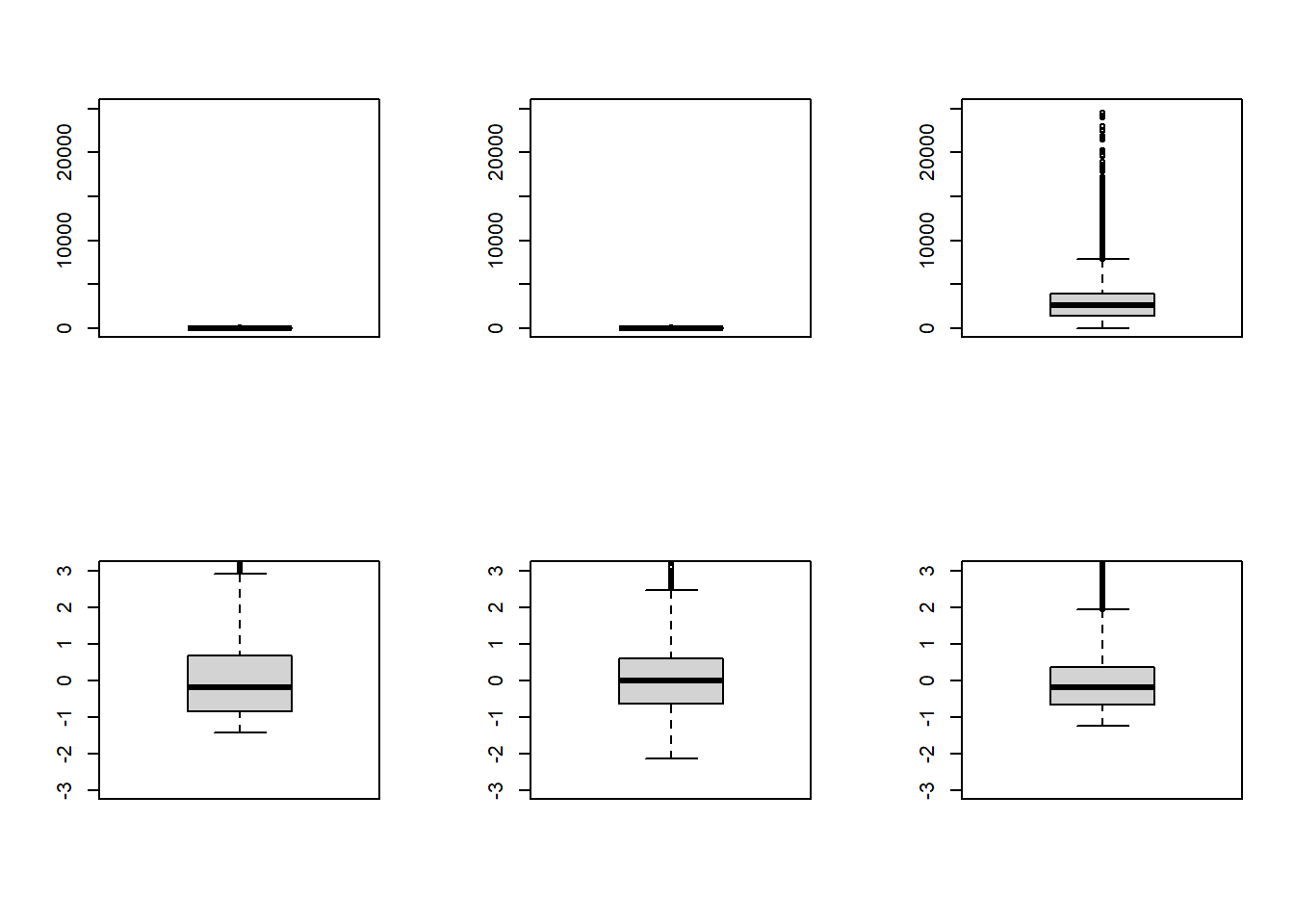

par(mfrow=c(2,3))
plot(density(eh19p$s02a_03))
plot(density(eh19p$tothrs,na.rm=T))
plot(density(eh19p$ylab,na.rm=T))

plot(density(x1))
plot(density(x2,na.rm=T))
plot(density(x3,na.rm=T))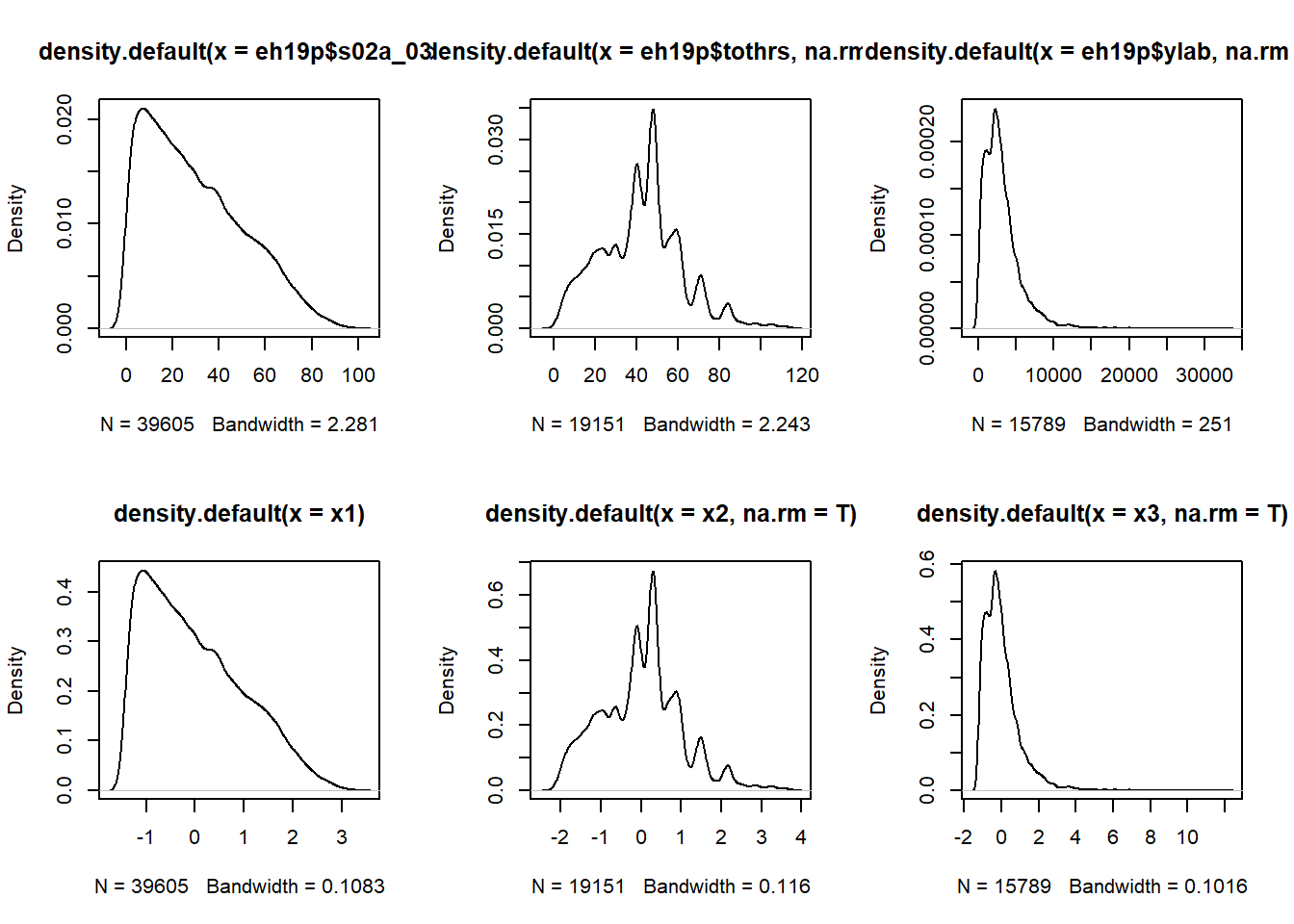

mean(eh19p$ylab,na.rm=T)

## [1] 3074.659

median(eh19p$ylab,na.rm=T)

## [1] 2598

Función logarítmo

dev.off()

## null device 
##           1

curve(log,xlim=c(10,30000))

x1<-log(eh19p$s02a_03)
x2<-log(eh19p$tothrs)
x3<-log(eh19p$ylab)

par(mfrow=c(2,3))
plot(density(eh19p$s02a_03))
plot(density(eh19p$tothrs,na.rm=T))
plot(density(eh19p$ylab,na.rm=T))

plot(density(x1))
plot(density(x2,na.rm=T))
plot(density(x3,na.rm=T))
dev.off()

## null device 
##           1

Creación de variables

eh19p$log_ylab <-log(eh19p$ylab)
eh19p$scale_ylab <-scale(eh19p$ylab)
names(eh19p)

##   [1] "folio"         
##   [2] "depto"         
##   [3] "area"          
##   [4] "nro"           
##   [5] "s02a_02"       
##   [6] "s02a_03"       
##   [7] "s02a_04a"      
##   [8] "s02a_04b"      
##   [9] "s02a_04c"      
##  [10] "s02a_05"       
##  [11] "s02a_06a"      
##  [12] "s02a_06b"      
##  [13] "s02a_06c"      
##  [14] "s02a_06d"      
##  [15] "s02a_06e"      
##  [16] "s02a_06_b"     
##  [17] "s02a_07_1"     
##  [18] "s02a_07_2"     
##  [19] "s02a_07_3"     
##  [20] "s02a_08"       
##  [21] "s02a_10"       
##  [22] "s03a_01a"      
##  [23] "s03a_01b"      
##  [24] "s03a_01c"      
##  [25] "s03a_01d"      
##  [26] "s03a_01d2_cod" 
##  [27] "s03a_01e"      
##  [28] "s03a_02"       
##  [29] "s03a_02e"      
##  [30] "s03a_03"       
##  [31] "s03a_03a"      
##  [32] "s03a_04"       
##  [33] "s03a_04npioc"  
##  [34] "s04a_01a"      
##  [35] "s04a_01b"      
##  [36] "s04a_01e"      
##  [37] "s04a_02a"      
##  [38] "s04a_02b"      
##  [39] "s04a_02e"      
##  [40] "s04a_03a"      
##  [41] "s04a_03b"      
##  [42] "s04a_03c"      
##  [43] "s04a_03d"      
##  [44] "s04a_03e"      
##  [45] "s04a_03f"      
##  [46] "s04a_03g"      
##  [47] "s04a_04a"      
##  [48] "s04a_04b"      
##  [49] "s04a_04e"      
##  [50] "S04A_0"        
##  [51] "S04A_1"        
##  [52] "S04A_2"        
##  [53] "s04a_05a"      
##  [54] "s04a_05b"      
##  [55] "s04a_05c"      
##  [56] "s04a_05d"      
##  [57] "s04a_05e"      
##  [58] "s04a_06a"      
##  [59] "s04a_07a"      
##  [60] "s04a_07a_e"    
##  [61] "s04a_06b"      
##  [62] "s04a_07b"      
##  [63] "s04a_07b_e"    
##  [64] "s04a_06c"      
##  [65] "s04a_07c"      
##  [66] "s04a_07c_e"    
##  [67] "s04a_06d"      
##  [68] "s04a_07d"      
##  [69] "s04a_07d_e"    
##  [70] "s04a_06e"      
##  [71] "s04a_07e"      
##  [72] "s04a_07e_e"    
##  [73] "s04a_06f"      
##  [74] "s04a_07f"      
##  [75] "s04a_07f_e"    
##  [76] "s04a_06g"      
##  [77] "s04a_07g"      
##  [78] "s04a_07g_e"    
##  [79] "s04a_08"       
##  [80] "s04a_08a1"     
##  [81] "s04a_08a2"     
##  [82] "s04a_08b"      
##  [83] "s04a_09"       
##  [84] "s04a_09a"      
##  [85] "s04b_11a"      
##  [86] "s04b_11b"      
##  [87] "s04b_12"       
##  [88] "s04b_13"       
##  [89] "s04b_14a"      
##  [90] "s04b_14b"      
##  [91] "s04b_15"       
##  [92] "s04b_15e"      
##  [93] "S04B_9"        
##  [94] "S04B_A"        
##  [95] "S04B_B"        
##  [96] "s04b_16"       
##  [97] "s04b_16e"      
##  [98] "S04B_6"        
##  [99] "S04B_7"        
## [100] "S04B_8"        
## [101] "s04b_17"       
## [102] "s04b_17e"      
## [103] "S04B_3"        
## [104] "S04B_4"        
## [105] "S04B_5"        
## [106] "s04b_18"       
## [107] "s04b_18e"      
## [108] "S04B_0"        
## [109] "S04B_1"        
## [110] "S04B_2"        
## [111] "s04b_19"       
## [112] "s04b_20a1"     
## [113] "s04b_20a2"     
## [114] "s04b_20b"      
## [115] "s04b_21a"      
## [116] "s04b_21b"      
## [117] "s04b_21b2"     
## [118] "s04c_22"       
## [119] "s04c_23"       
## [120] "s04d_24"       
## [121] "s04d_25"       
## [122] "s04d_26"       
## [123] "s04d_27a"      
## [124] "s04d_27b"      
## [125] "s04e_28a"      
## [126] "s04e_28b"      
## [127] "s04e_29a"      
## [128] "s04e_29b"      
## [129] "s04e_30a"      
## [130] "s04e_30b"      
## [131] "s04e_30c_cod"  
## [132] "s04e_31a"      
## [133] "s04e_31b"      
## [134] "s04e_31c"      
## [135] "s04e_31d"      
## [136] "s04e_31e"      
## [137] "s04e_31f"      
## [138] "s04e_31_e"     
## [139] "s04e_32a"      
## [140] "s04e_32b"      
## [141] "s04e_33a"      
## [142] "s04e_33b"      
## [143] "s04_e_34a"     
## [144] "s04f_34"       
## [145] "s04f_35a"      
## [146] "s04f_35b"      
## [147] "s04f_35c"      
## [148] "s04f_35e"      
## [149] "s05a_01"       
## [150] "s05a_01a"      
## [151] "s05a_02a"      
## [152] "s05a_02c"      
## [153] "s05a_03a"      
## [154] "s05a_03c"      
## [155] "s05a_04"       
## [156] "s05a_05"       
## [157] "s05a_05_e"     
## [158] "s05a_06a"      
## [159] "s05a_06c"      
## [160] "s05a_07a"      
## [161] "s05a_07b"      
## [162] "s05a_08"       
## [163] "s05a_09"       
## [164] "s05b_10"       
## [165] "s05b_11"       
## [166] "s05b_11_e"     
## [167] "s05b_11a"      
## [168] "s05c_13a"      
## [169] "s05c_13b"      
## [170] "s05c_13c"      
## [171] "s05c_13d"      
## [172] "s05c_13e"      
## [173] "s05c_13f"      
## [174] "s05c_13g"      
## [175] "s05c_13h"      
## [176] "s05c_13_e"     
## [177] "s05c_14a"      
## [178] "s05c_14b"      
## [179] "s05c_15a"      
## [180] "s05c_15b"      
## [181] "s05d_17"       
## [182] "s05d_18"       
## [183] "s05d_19a"      
## [184] "s05d_19b"      
## [185] "s05d_20a"      
## [186] "s05d_20b"      
## [187] "s05d_21a"      
## [188] "s05d_21b"      
## [189] "s05d_21e"      
## [190] "s05d_22a"      
## [191] "s05d_22b"      
## [192] "s05d_22c"      
## [193] "s05d_22d"      
## [194] "s05d_22e"      
## [195] "s05d_22f"      
## [196] "s05d_22g"      
## [197] "s05d_22h"      
## [198] "s05d_22i"      
## [199] "s05d_22j"      
## [200] "s05d_22k"      
## [201] "s05d_22l"      
## [202] "s05d_22_e"     
## [203] "s06a_01"       
## [204] "s06a_02"       
## [205] "s06a_03"       
## [206] "s06a_04"       
## [207] "s06a_05"       
## [208] "s06a_06aa"     
## [209] "s06a_06ab"     
## [210] "s06a_06ac"     
## [211] "s06a_06e"      
## [212] "s06a_07"       
## [213] "s06a_08a"      
## [214] "s06a_08b"      
## [215] "s06a_09"       
## [216] "s06a_09e"      
## [217] "s06a_10"       
## [218] "s06a_10e"      
## [219] "s06b_11a"      
## [220] "s06b_11a_cod"  
## [221] "s06b_11b"      
## [222] "s06b_12a"      
## [223] "s06b_12a_cod"  
## [224] "s06b_12b"      
## [225] "s06b_13"       
## [226] "s06b_13a"      
## [227] "s06b_13b"      
## [228] "s06b_13c"      
## [229] "s06b_14"       
## [230] "s06b_15aa"     
## [231] "s06b_15ab"     
## [232] "s06b_15ba"     
## [233] "s06b_15bb"     
## [234] "s06b_15ca"     
## [235] "s06b_15cb"     
## [236] "s06b_15da"     
## [237] "s06b_15db"     
## [238] "s06b_17"       
## [239] "s06b_18"       
## [240] "s06b_19a"      
## [241] "s06b_19b"      
## [242] "s06b_20"       
## [243] "s06b_20e"      
## [244] "s06b_21a"      
## [245] "s06b_21b"      
## [246] "s06b_22"       
## [247] "s06b_23aa"     
## [248] "s06b_23ab"     
## [249] "s06c_25a"      
## [250] "s06c_25b"      
## [251] "s06c_26a"      
## [252] "s06c_26b"      
## [253] "s06c_27aa"     
## [254] "s06c_27ab"     
## [255] "s06c_27ba"     
## [256] "s06c_27bb"     
## [257] "s06c_28a"      
## [258] "s06c_28a1"     
## [259] "s06c_28b"      
## [260] "s06c_29a"      
## [261] "s06c_29b"      
## [262] "s06c_30a"      
## [263] "s06c_30a1"     
## [264] "s06c_30a2"     
## [265] "s06c_30b"      
## [266] "s06c_30b1"     
## [267] "s06c_30b2"     
## [268] "s06c_30c"      
## [269] "s06c_30c1"     
## [270] "s06c_30c2"     
## [271] "s06c_30d"      
## [272] "s06c_30d1"     
## [273] "s06c_30d2"     
## [274] "s06c_30e"      
## [275] "s06c_30e1"     
## [276] "s06c_30e2"     
## [277] "s06d_31a"      
## [278] "s06d_31b"      
## [279] "s06d_32aa"     
## [280] "s06d_32ab"     
## [281] "s06d_32ba"     
## [282] "s06d_32bb"     
## [283] "s06d_32ca"     
## [284] "s06d_32cb"     
## [285] "s06d_32da"     
## [286] "s06d_32db"     
## [287] "s06d_32ea"     
## [288] "s06d_32eb"     
## [289] "s06d_32fa"     
## [290] "s06d_32fb"     
## [291] "s06d_32ga"     
## [292] "s06d_32gb"     
## [293] "s06d_32ha"     
## [294] "s06d_32hb"     
## [295] "s06d_33a"      
## [296] "s06d_33b"      
## [297] "s06d_34"       
## [298] "s06e_35a"      
## [299] "s06e_35a_cod"  
## [300] "s06e_35b"      
## [301] "s06e_36"       
## [302] "s06e_37"       
## [303] "s06e_38a"      
## [304] "s06e_38b"      
## [305] "s06e_39"       
## [306] "s06e_40"       
## [307] "s06e_40b"      
## [308] "s06f_42a"      
## [309] "s06f_42b"      
## [310] "s06f_43a"      
## [311] "s06f_43a1"     
## [312] "s06f_43b"      
## [313] "s06f_43b1"     
## [314] "s06f_43c"      
## [315] "s06f_43c1"     
## [316] "s06f_44a"      
## [317] "s06f_44b"      
## [318] "s06f_45aa"     
## [319] "s06f_45ab"     
## [320] "s06f_45ba"     
## [321] "s06f_45bb"     
## [322] "s06f_45ca"     
## [323] "s06f_45cb"     
## [324] "s06f_45da"     
## [325] "s06f_45db"     
## [326] "s06f_45ea"     
## [327] "s06f_45eb"     
## [328] "s06f_45fa"     
## [329] "s06f_45fb"     
## [330] "s06f_45ga"     
## [331] "s06f_45gb"     
## [332] "s06f_45ha"     
## [333] "s06f_45hb"     
## [334] "s06f_46a"      
## [335] "s06f_46b"      
## [336] "s06g_47"       
## [337] "s06g_48"       
## [338] "s06g_49"       
## [339] "s06g_49e"      
## [340] "s06g_50"       
## [341] "s06g_50e"      
## [342] "s06g_51"       
## [343] "s06g_51e"      
## [344] "s06g_52"       
## [345] "s06g_53"       
## [346] "s06g_54"       
## [347] "s06g_55"       
## [348] "s07a_01a"      
## [349] "s07a_01b"      
## [350] "s07a_01c"      
## [351] "s07a_01d"      
## [352] "s07a_01e"      
## [353] "s07a_01e0"     
## [354] "s07a_01e1"     
## [355] "s07a_01e1e"    
## [356] "s07a_01e2"     
## [357] "s07a_01e2e"    
## [358] "s07a_02a"      
## [359] "s07a_02b"      
## [360] "s07a_02c"      
## [361] "s07a_02ce"     
## [362] "s07a_03a"      
## [363] "s07a_03b"      
## [364] "s07a_03c"      
## [365] "s07a_04a"      
## [366] "s07a_04b"      
## [367] "s07a_04c"      
## [368] "s07a_04d"      
## [369] "s07b_05aa"     
## [370] "s07b_05ab"     
## [371] "s07b_05ba"     
## [372] "s07b_05bb"     
## [373] "s07b_05ca"     
## [374] "s07b_05cb"     
## [375] "s07b_05da"     
## [376] "s07b_05db"     
## [377] "s07b_05de"     
## [378] "s07b_05ea"     
## [379] "s07b_05eb"     
## [380] "s07b_05ee"     
## [381] "s07c_06"       
## [382] "s07c_07"       
## [383] "s07c_08a"      
## [384] "s07c_08b"      
## [385] "s07c_08e"      
## [386] "s07c_09"       
## [387] "s07c_09e"      
## [388] "s07c_10"       
## [389] "s08a_01"       
## [390] "s08a_03a"      
## [391] "s08a_03b"      
## [392] "s08a_03c"      
## [393] "s08a_03e"      
## [394] "s08a_04"       
## [395] "s08a_06"       
## [396] "upm"           
## [397] "estrato"       
## [398] "factor"        
## [399] "tipohogar"     
## [400] "cobersalud"    
## [401] "hnv_ult_a"     
## [402] "quienatenparto"
## [403] "dondeatenparto"
## [404] "niv_ed"        
## [405] "niv_ed_g"      
## [406] "cmasi"         
## [407] "educ_prev"     
## [408] "aestudio"      
## [409] "cob_op"        
## [410] "caeb_op"       
## [411] "pet"           
## [412] "ocupado"       
## [413] "cesante"       
## [414] "aspirante"     
## [415] "desocupado"    
## [416] "pea"           
## [417] "temporal"      
## [418] "permanente"    
## [419] "pei"           
## [420] "condact"       
## [421] "phrs"          
## [422] "shrs"          
## [423] "tothrs"        
## [424] "yprilab"       
## [425] "yseclab"       
## [426] "ylab"          
## [427] "ynolab"        
## [428] "yper"          
## [429] "yhog"          
## [430] "yhogpc"        
## [431] "z"             
## [432] "zext"          
## [433] "p0"            
## [434] "p1"            
## [435] "p2"            
## [436] "pext0"         
## [437] "pext1"         
## [438] "pext2"         
## [439] "log_ylab"      
## [440] "scale_ylab"

#install.packages("dplyr")
library(dplyr) # filtrado, selección, creación de variables, resumen
#nota: dplyr se enfoca en el encadenamiento de comandos, con una lógica similar al SQL

# %>% # operador pipe: ctr + mayus + m 

eh19p <- eh19p %>% mutate(x1=ylab^2,llylab=log(ylab),
                 tothrs_mensual=tothrs*4.35,mujer=s02a_02=="2.Mujer")

#cut() # crear clases

# grandes grupos de edad
eh19p<-eh19p %>% mutate(gedad=cut(s02a_03,c(-1,18,60,max(s02a_03)),labels = c("<=18","19 a 60",">60") ))

eh19p %>% select(1,folio,s02a_03,gedad) %>% head()

##                    folio s02a_03
## 1 111-00416110273-A-0021      42
## 2 111-00416110273-A-0021      36
## 3 111-00416110273-A-0021      19
## 4 111-00416110273-A-0021      13
## 5 111-00416110273-A-0021       3
## 6 111-00416110273-A-0021      86
##     gedad
## 1 19 a 60
## 2 19 a 60
## 3 19 a 60
## 4    <=18
## 5    <=18
## 6     >60

table(eh19p$gedad)

## 
##    <=18 19 a 60     >60 
##   14831   20736    4038

eh19p %>% select(gedad) %>% table()

## gedad
##    <=18 19 a 60     >60 
##   14831   20736    4038

barplot(table(eh19p$gedad))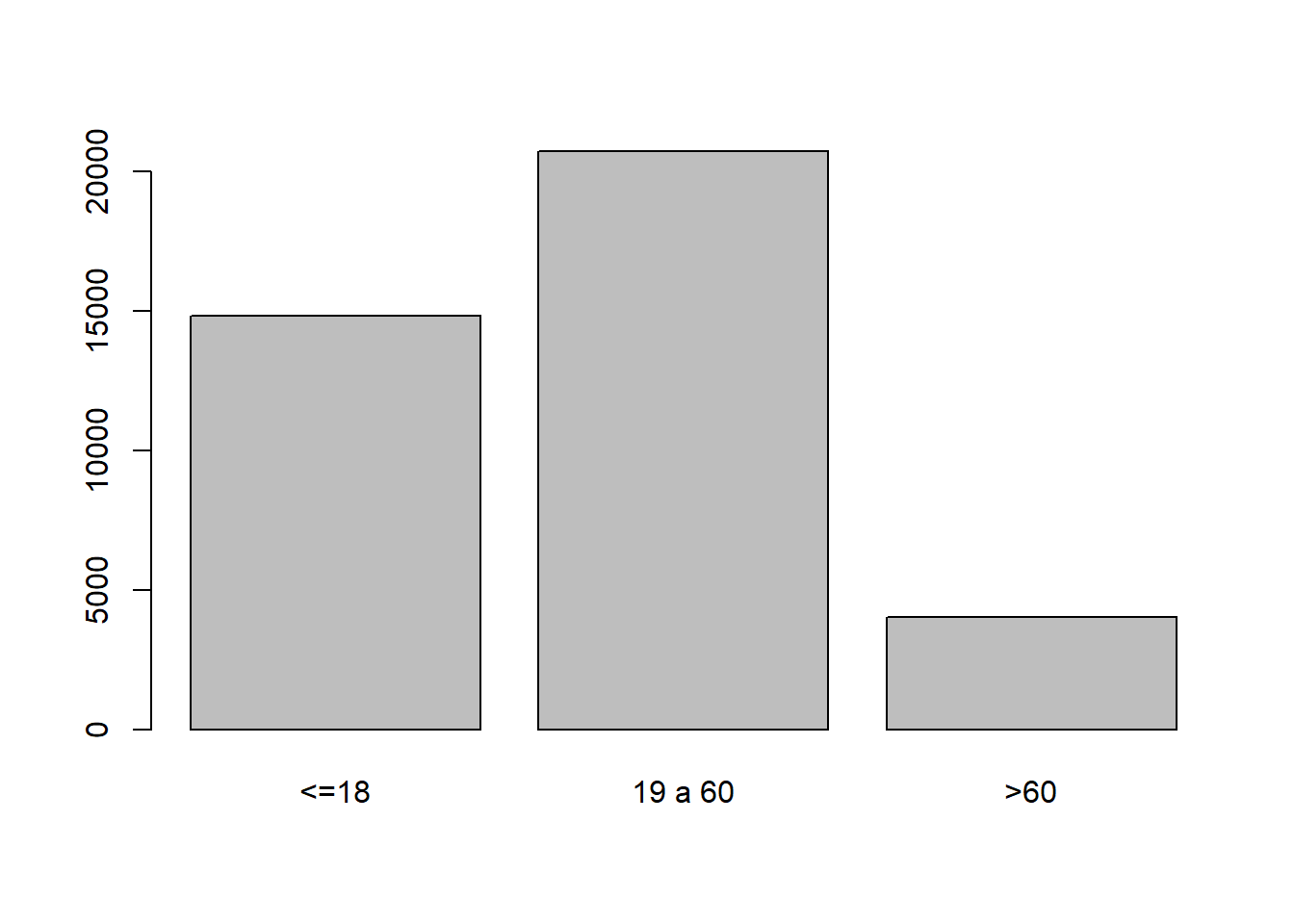

Recodificar variables

load(url("https://github.com/AlvaroLimber/EST-384/raw/master/data/eh19.RData"))
library(dplyr)

a<-c(1:10)
recode(a,`1` = 20L,`2` = 20L,`4` = 30L)

eh19p$sexo<-recode(eh19p$s02a_02,"1.Hombre"="H","2.Mujer"="M")

table(eh19p$sexo)

eh19p<-eh19p %>% mutate(sexo2=recode(s02a_02,"1.Hombre"="M","2.Mujer"="F"))
eh19p %>% select(sexo2) %>% table()

# binarias
unique(eh19p$depto)
# se quiere crear una nueva variable, llamada región: 
#    Altiplano: LP, OR, PT
#    Valle: CB, CH, TR
#    Llano: SC, BN, PD
# tarea
#if_else() # trabaja con spark, para crear binarios
#case_when() # múltiple categorías basadas en reglas

v1<-c("La Paz","Oruro","Potosí")
v2<-c("Chuquisaca","Cochabamba","Tarija")
v3<-c("Santa Cruz","Beni","Pando")

eh19p %>% mutate(altiplano = depto %in% v1 ) %>% select(altiplano) %>% table()
  
eh19p <- eh19p %>% mutate(altiplano = depto %in% v1 , valle = depto %in% v2,llano = depto %in% v3)
names(eh19p)

1.6.11 Definir diseño de encuesta por muestreo

Si tenemos una base de datos proveniente de una encuesta por muestreo, debemos tener conocimiento de las características del diseño muestral empleado en la encuesta, ya que este diseño afecta de forma directa el proceso de estimación y tiene un error de muestreo. Principalmente lo siguiente:

Si el diseño tiene etapas (o mono etápico con conglomerados), la variable de conglomeración y de estratificación son muy relevantes. Estas afectan directamente a los errores de las estimaciones.
Si el esquema de selección de las unidades muestrales a sido autoponderada (MAS, todas las unidades tenían la misma probabilidad de ser seleccionadas) o no. Si no es autponderada se requiere la variable conocida como el factor de expansión (inverso de la probabilidad de selección)

Hay tres variables relevantes: conglomerados (principalmente primera etapa), estratificación (principalmente primera etapa) y factor de expansión.

Idealmente en un muestreo de varias etapas y estratificado el factor por finitud es necesario ya que permite mejorar la aproximación a la varianza.

#install.packages("survey")
library(survey) # no trabaja con el concepto de dplyr, no permite el uso de "%>%" 
library(srvyr) # permite el uso del operador %>% 
names(eh19p)
#survey
sd_eh19p<-svydesign(ids = ~upm + folio, strata = ~estrato, weights = ~factor,data = eh19p)
str(sd_eh19p)

table(eh19p$p0)
prop.table(table(eh19p$p0))*100 # pobreza moderada en la muestra 

svytable(~p0 ,design = sd_eh19p)
prop.table(svytable(~p0 ,design = sd_eh19p))*100

summary(svytable(~p0 ,design = sd_eh19p))

t1<-svymean(~ylab,design = sd_eh19p,na.rm=T,deff=T)
cv(t1)
confint(t1)

t2<-svyby(~ylab,by=~depto+area,design = sd_eh19p,FUN = svymean,na.rm=T)
cv(t2)
confint(t2)

summary(svytable(~depto+p0 ,design = sd_eh19p)) # revisar

# departamento
prop.table(table(eh19p$depto,eh19p$p0),1)*100
prop.table(svytable(~depto+p0 ,design = sd_eh19p),1)*100

svydesign(ids=~1,data=bd)#mas
svydesign(ids=~1,strata = estrato,data=bd)#mas estraficado
svydesign(ids=~1,strata = ~estrato,weights = ~ponderador,data=bd)#pps estraficado

svymean(~p0, design=sd_eh19p,na.rm=T)
svytotal(~p0, design=sd_eh19p,na.rm=T)

#
svytable(~p0,design=sd_eh19p) # tablas de contigencias y hacer pruebas sobre estas

t1<-svymean(~p0,design=sd_eh19p,na.rm=T) # proporciones / medias
t2<-svytotal(~p0,design=sd_eh19p,na.rm=T) # totales clase / total

cv(t1)
cv(t2)

confint(t1)
confint(t2)

sd2_eh19p<-svydesign(ids = ~1, weights = ~factor,data = eh19p) # pps

t3<-svymean(~p0,design=sd2_eh19p,na.rm=T) # proporciones / medias

t1
t3
cv(t1)*100
cv(t3)*100

summary(lm(ylab~aestudio,data=eh19p)) # ingreso= B0+B1*aestudio+e OLS
summary(lm(ylab~aestudio,data=eh19p,weights = factor )) # Minimos cuadrados ponderados

m1<-svyglm(ylab~aestudio,design=sd_eh19p)
summary(m1)
install.packages("jtools")

library(jtools)
summ(m1)

psrsq(m1)

# srvyr 

library(srvyr)
sd3_eh19p<-as_survey_design(sd_eh19p)

sd_eh19p %>% select(p0) %>% svymean()

sd3_eh19p %>% summarise(survey_mean(s02a_03))

sd3_eh19p %>% group_by(depto,area,s02a_02) %>% summarise(m_edad=survey_mean(s02a_03))

sd3_eh19p %>% group_by(depto,area,s02a_02) %>% summarise(m_edad=survey_mean(s02a_03),m_ylab=survey_mean(ylab,na.rm=T))

# p0
sd3_eh19p %>% group_by(depto) %>% survey_tally()

sd3_eh19p %>% group_by(depto) %>% survey_count()

sd3_eh19p %>% mutate(pobreza=p0=="Pobre") %>% summarise(p0=survey_mean(pobreza,na.rm=T))

sd3_eh19p %>% mutate(pobreza=p0=="Pobre") %>% group_by(depto,area) %>%  summarise(p0=survey_mean(pobreza,na.rm=T),N=survey_total(pobreza,na.rm=T))

sd4_eh19p<- eh19p %>% as_survey_design(ids=c(upm,folio),strata=estrato,weights=factor)

sd4_eh19p<- eh19p %>% as_survey_design(ids=upm,strata=estrato,weights=factor)

sd4_eh19p %>% mutate(pobreza=p0=="Pobre") %>% group_by(depto,area) %>%  summarise(p0=survey_mean(pobreza,na.rm=T,vartype = c("se", "ci", "var", "cv"),deff=T))

sd4_eh19p %>% mutate(pobreza=p0=="Pobre") %>%  summarise(p0=survey_mean(pobreza,na.rm=T,vartype = c("se", "ci", "var", "cv"),deff=T))

1.7 Imputación de variables

We should be suspicious of any dataset (large or small) which appears perfect.

— David J. Hand

1.7.1 La falta de información es información

MCAR missing completely at random
MAR missing at random
MNAR missing not at random

1.7.2 Aproximación formal

Sea $Y$ una matriz de datos con $n$ observaciones y $p$ variables. Sea $R$ una matriz de respuesta binaria, tal que si $y_{ij}$ es observada, entonces $r_{ij}=1$.

Los valores observados son colectados en $Y_{obs}$, las observaciones perdidas en $Y_{mis}$. Así, $Y=(Y_{obs},Y_{mis})$.

La distribución de $R$ depende de $Y=(Y_{obs},Y_{mis})$. Sea $\psi$ que contiene los parámetros del modelo de los datos perdidos, así la expresión del modelo de los datos perdidos es $\Pr(R|Y_\mathrm{obs},Y_\mathrm{mis},\psi)$

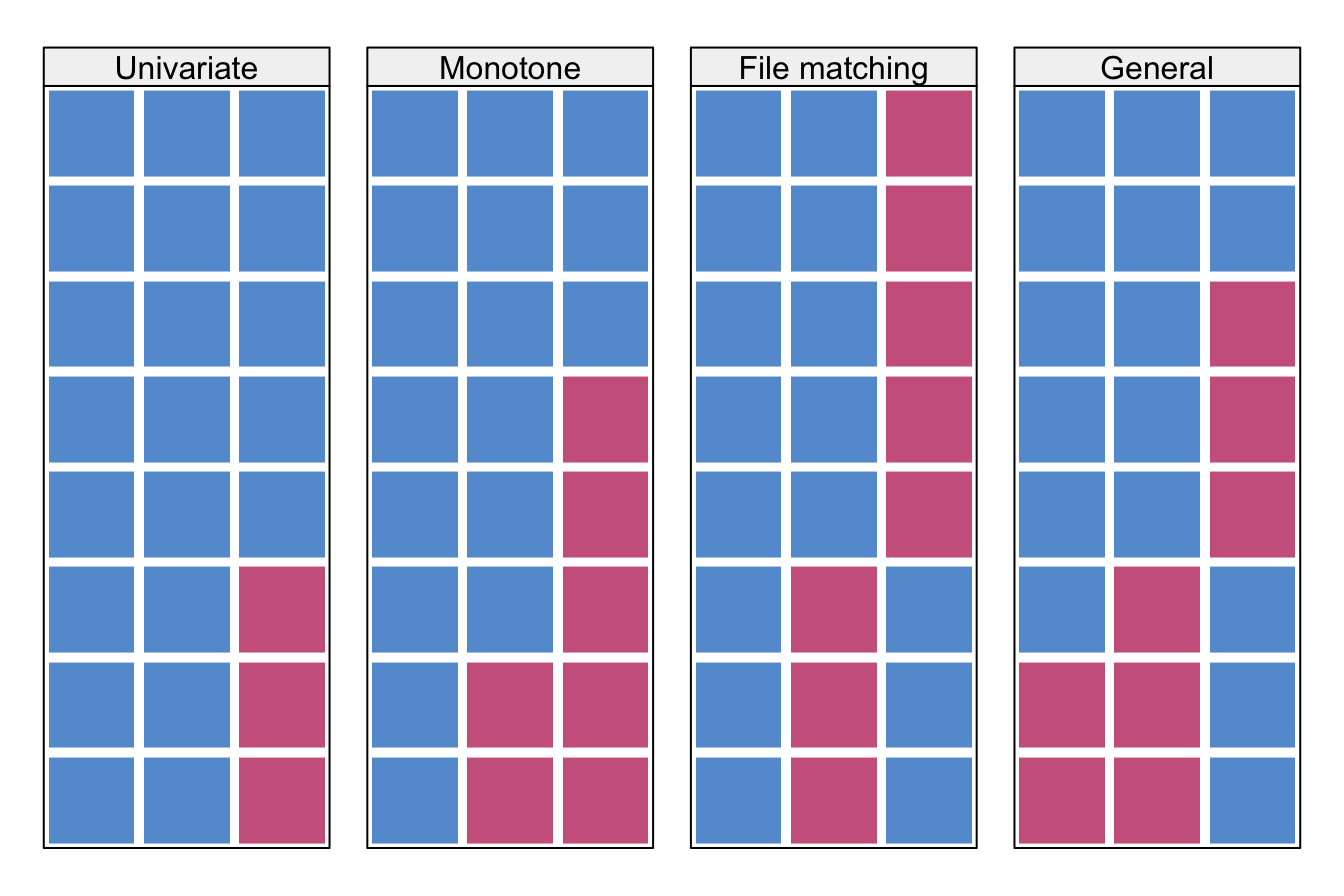
1.7.3 MCAR, MAR, MNAR

MCAR (missing completely at random ) \[ \Pr(R=0|{\mbox{$Y_\mathrm{obs}$}},{\mbox{$Y_\mathrm{mis}$}},\psi) = \Pr(R=0|\psi) \]

MAR (missing at random ) \[ \Pr(R=0|{\mbox{$Y_\mathrm{obs}$}},{\mbox{$Y_\mathrm{mis}$}},\psi) = \Pr(R=0|{\mbox{$Y_\mathrm{obs}$}},\psi) \]

MNAR (missing not at random ) \[ \Pr(R=0|{\mbox{$Y_\mathrm{obs}$}},{\mbox{$Y_\mathrm{mis}$}},\psi) \]

1.7.4 Alternativas para trabajar con los Missings (Ad-hoc)

Listwise deletion
Pairwise deletion
Mean imputation
Regression imputation
Stochastic regression imputation
Last observation carried forward (LOCF) and baseline observation carried forward (BOCF)
Indicator method

1.7.5 Imputación Multiple

1.7.6 Patrones en datos multivariados

1.7.7 Influx and outflux

\[ I_j = \frac{\sum_j^p\sum_k^p\sum_i^n (1-r_{ij})r_{ik}}{\sum_k^p\sum_i^n r_{ik}} \]

La variable con mayor influx está mejor conectada a los datos observados y, por lo tanto, podría ser más fácil de imputar.

\[ O_j = \frac{\sum_j^p\sum_k^p\sum_i^n r_{ij}(1-r_{ik})}{\sum_k^p\sum_i^n 1-r_{ij}} \] La variable con mayor outflux está mejor conectada a los datos faltantes, por lo tanto, es potencialmente más útil para imputar otras variables.

1.7.8 Imputación de datos monótonos

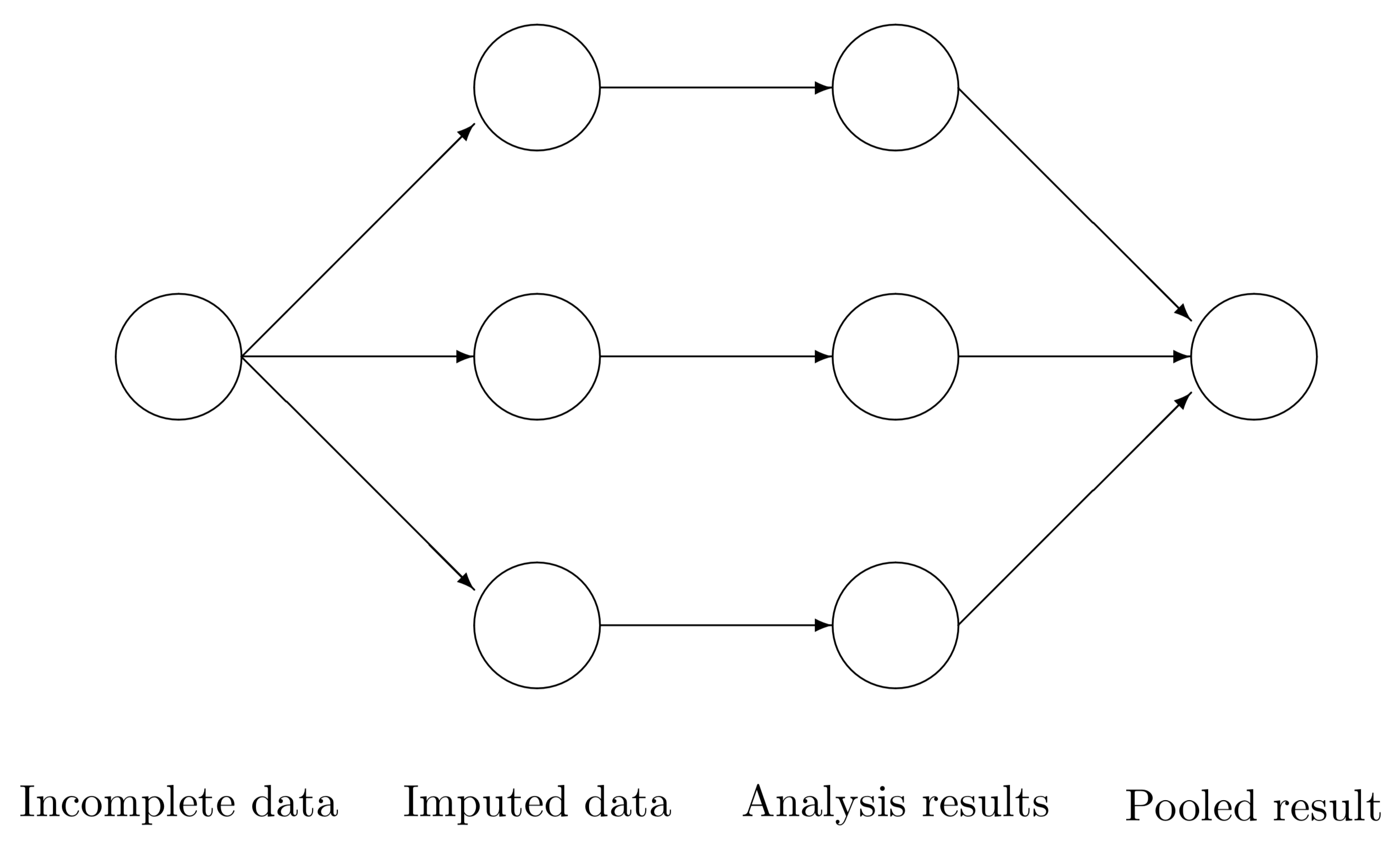
1.7.9 Multivariate Imputation by Chained Equations (mice)

(Imputación multivariante por ecuaciones encadenadas)

1.7.10 En R

1.7.10.1 Métodos ad-hoc

Listwise deletion (trabajar solo con casos completos)

table(is.na(airquality$Ozone))

## 
## FALSE  TRUE 
##   116    37

R<-(!is.na(airquality))*1

mean(airquality$Ozone)

## [1] NA

#listwise
x<-na.omit(airquality$Ozone)
mean(x)

## [1] 42.12931

bd<-airquality
bd2<-na.omit(bd)

na.action(x)

##  [1]   5  10  25  26  27  32  33
##  [8]  34  35  36  37  39  42  43
## [15]  45  46  52  53  54  55  56
## [22]  57  58  59  60  61  65  72
## [29]  75  83  84 102 103 107 115
## [36] 119 150
## attr(,"class")
## [1] "omit"

na.action(bd2)

##   5   6  10  11  25  26  27  32 
##   5   6  10  11  25  26  27  32 
##  33  34  35  36  37  39  42  43 
##  33  34  35  36  37  39  42  43 
##  45  46  52  53  54  55  56  57 
##  45  46  52  53  54  55  56  57 
##  58  59  60  61  65  72  75  83 
##  58  59  60  61  65  72  75  83 
##  84  96  97  98 102 103 107 115 
##  84  96  97  98 102 103 107 115 
## 119 150 
## 119 150 
## attr(,"class")
## [1] "omit"

naprint(na.action(x))

## [1] "37 observations deleted due to missingness"

naprint(na.action(bd2))

## [1] "42 observations deleted due to missingness"

table(complete.cases(bd))

## 
## FALSE  TRUE 
##    42   111

ii<-complete.cases(bd)

bd[ii,]

##     Ozone Solar.R Wind Temp Month
## 1      41     190  7.4   67     5
## 2      36     118  8.0   72     5
## 3      12     149 12.6   74     5
## 4      18     313 11.5   62     5
## 7      23     299  8.6   65     5
## 8      19      99 13.8   59     5
## 9       8      19 20.1   61     5
## 12     16     256  9.7   69     5
## 13     11     290  9.2   66     5
## 14     14     274 10.9   68     5
## 15     18      65 13.2   58     5
## 16     14     334 11.5   64     5
## 17     34     307 12.0   66     5
## 18      6      78 18.4   57     5
## 19     30     322 11.5   68     5
## 20     11      44  9.7   62     5
## 21      1       8  9.7   59     5
## 22     11     320 16.6   73     5
## 23      4      25  9.7   61     5
## 24     32      92 12.0   61     5
## 28     23      13 12.0   67     5
## 29     45     252 14.9   81     5
## 30    115     223  5.7   79     5
## 31     37     279  7.4   76     5
## 38     29     127  9.7   82     6
## 40     71     291 13.8   90     6
## 41     39     323 11.5   87     6
## 44     23     148  8.0   82     6
## 47     21     191 14.9   77     6
## 48     37     284 20.7   72     6
## 49     20      37  9.2   65     6
## 50     12     120 11.5   73     6
## 51     13     137 10.3   76     6
## 62    135     269  4.1   84     7
## 63     49     248  9.2   85     7
## 64     32     236  9.2   81     7
## 66     64     175  4.6   83     7
## 67     40     314 10.9   83     7
## 68     77     276  5.1   88     7
## 69     97     267  6.3   92     7
## 70     97     272  5.7   92     7
## 71     85     175  7.4   89     7
## 73     10     264 14.3   73     7
## 74     27     175 14.9   81     7
## 76      7      48 14.3   80     7
## 77     48     260  6.9   81     7
## 78     35     274 10.3   82     7
## 79     61     285  6.3   84     7
## 80     79     187  5.1   87     7
## 81     63     220 11.5   85     7
## 82     16       7  6.9   74     7
## 85     80     294  8.6   86     7
## 86    108     223  8.0   85     7
## 87     20      81  8.6   82     7
## 88     52      82 12.0   86     7
## 89     82     213  7.4   88     7
## 90     50     275  7.4   86     7
## 91     64     253  7.4   83     7
## 92     59     254  9.2   81     7
## 93     39      83  6.9   81     8
## 94      9      24 13.8   81     8
## 95     16      77  7.4   82     8
## 99    122     255  4.0   89     8
## 100    89     229 10.3   90     8
## 101   110     207  8.0   90     8
## 104    44     192 11.5   86     8
## 105    28     273 11.5   82     8
## 106    65     157  9.7   80     8
## 108    22      71 10.3   77     8
## 109    59      51  6.3   79     8
## 110    23     115  7.4   76     8
## 111    31     244 10.9   78     8
## 112    44     190 10.3   78     8
## 113    21     259 15.5   77     8
## 114     9      36 14.3   72     8
## 116    45     212  9.7   79     8
## 117   168     238  3.4   81     8
## 118    73     215  8.0   86     8
## 120    76     203  9.7   97     8
## 121   118     225  2.3   94     8
## 122    84     237  6.3   96     8
## 123    85     188  6.3   94     8
## 124    96     167  6.9   91     9
## 125    78     197  5.1   92     9
## 126    73     183  2.8   93     9
## 127    91     189  4.6   93     9
## 128    47      95  7.4   87     9
## 129    32      92 15.5   84     9
## 130    20     252 10.9   80     9
## 131    23     220 10.3   78     9
## 132    21     230 10.9   75     9
## 133    24     259  9.7   73     9
## 134    44     236 14.9   81     9
## 135    21     259 15.5   76     9
## 136    28     238  6.3   77     9
## 137     9      24 10.9   71     9
## 138    13     112 11.5   71     9
## 139    46     237  6.9   78     9
## 140    18     224 13.8   67     9
## 141    13      27 10.3   76     9
## 142    24     238 10.3   68     9
## 143    16     201  8.0   82     9
## 144    13     238 12.6   64     9
## 145    23      14  9.2   71     9
## 146    36     139 10.3   81     9
## 147     7      49 10.3   69     9
## 148    14      20 16.6   63     9
## 149    30     193  6.9   70     9
## 151    14     191 14.3   75     9
## 152    18     131  8.0   76     9
## 153    20     223 11.5   68     9
##     Day
## 1     1
## 2     2
## 3     3
## 4     4
## 7     7
## 8     8
## 9     9
## 12   12
## 13   13
## 14   14
## 15   15
## 16   16
## 17   17
## 18   18
## 19   19
## 20   20
## 21   21
## 22   22
## 23   23
## 24   24
## 28   28
## 29   29
## 30   30
## 31   31
## 38    7
## 40    9
## 41   10
## 44   13
## 47   16
## 48   17
## 49   18
## 50   19
## 51   20
## 62    1
## 63    2
## 64    3
## 66    5
## 67    6
## 68    7
## 69    8
## 70    9
## 71   10
## 73   12
## 74   13
## 76   15
## 77   16
## 78   17
## 79   18
## 80   19
## 81   20
## 82   21
## 85   24
## 86   25
## 87   26
## 88   27
## 89   28
## 90   29
## 91   30
## 92   31
## 93    1
## 94    2
## 95    3
## 99    7
## 100   8
## 101   9
## 104  12
## 105  13
## 106  14
## 108  16
## 109  17
## 110  18
## 111  19
## 112  20
## 113  21
## 114  22
## 116  24
## 117  25
## 118  26
## 120  28
## 121  29
## 122  30
## 123  31
## 124   1
## 125   2
## 126   3
## 127   4
## 128   5
## 129   6
## 130   7
## 131   8
## 132   9
## 133  10
## 134  11
## 135  12
## 136  13
## 137  14
## 138  15
## 139  16
## 140  17
## 141  18
## 142  19
## 143  20
## 144  21
## 145  22
## 146  23
## 147  24
## 148  25
## 149  26
## 151  28
## 152  29
## 153  30

Y_obs<-na.omit(bd)
Y_mis<-mice::ic(bd)

bd$Ozone[bd$Ozone=="**"]<-NA
#gsub recode

table(R[,1],R[,2])

##    
##       0   1
##   0   2  35
##   1   5 111

chisq.test(table(R[,1],R[,2]))

## Warning in chisq.test(table(R[, 1],
## R[, 2])): Chi-squared approximation
## may be incorrect

## 
##  Pearson's Chi-squared test
##  with Yates' continuity
##  correction
## 
## data:  table(R[, 1], R[, 2])
## X-squared = 1.799e-29, df = 1,
## p-value = 1

apply(R,2,mean)

##     Ozone   Solar.R      Wind 
## 0.7581699 0.9542484 1.0000000 
##      Temp     Month       Day 
## 1.0000000 1.0000000 1.0000000

table(R[,1],R[,3])

##    
##       1
##   0  37
##   1 116

chisq.test(table(R[,1],R[,3]))

## 
##  Chi-squared test for given
##  probabilities
## 
## data:  table(R[, 1], R[, 3])
## X-squared = 40.791, df = 1,
## p-value = 1.694e-10

table(R[,1],R[,4])

##    
##       1
##   0  37
##   1 116

chisq.test(table(R[,1],R[,4]))

## 
##  Chi-squared test for given
##  probabilities
## 
## data:  table(R[, 1], R[, 4])
## X-squared = 40.791, df = 1,
## p-value = 1.694e-10

R<-as.data.frame(R)
m1<-glm(Ozone~Solar.R,data = R,family = "binomial") # logit

summary(m1)

## 
## Call:
## glm(formula = Ozone ~ Solar.R, family = "binomial", data = R)
## 
## Deviance Residuals: 
##     Min       1Q   Median  
## -1.6901   0.7404   0.7404  
##      3Q      Max  
##  0.7404   0.8203  
## 
## Coefficients:
##             Estimate Std. Error
## (Intercept)   0.9163     0.8367
## Solar.R       0.2379     0.8588
##             z value Pr(>|z|)
## (Intercept)   1.095    0.273
## Solar.R       0.277    0.782
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 169.27  on 152  degrees of freedom
## Residual deviance: 169.20  on 151  degrees of freedom
## AIC: 173.2
## 
## Number of Fisher Scoring iterations: 4

summary(lm(Ozone~Solar.R,data=bd2))

## 
## Call:
## lm(formula = Ozone ~ Solar.R, data = bd2)
## 
## Residuals:
##     Min      1Q  Median      3Q 
## -48.292 -21.361  -8.864  16.373 
##     Max 
## 119.136 
## 
## Coefficients:
##             Estimate Std. Error
## (Intercept) 18.59873    6.74790
## Solar.R      0.12717    0.03278
##             t value Pr(>|t|)    
## (Intercept)   2.756 0.006856 ** 
## Solar.R       3.880 0.000179 ***
## ---
## Signif. codes:  
##   0 '***' 0.001 '**' 0.01 '*'
##   0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 31.33 on 109 degrees of freedom
## Multiple R-squared:  0.1213, Adjusted R-squared:  0.1133 
## F-statistic: 15.05 on 1 and 109 DF,  p-value: 0.0001793

Pairwise deletion (casos parciales)

dim(na.omit(airquality[,1:2]))

## [1] 111   2

dim(na.omit(airquality[,c(1,3)]))

## [1] 116   2

dim(na.omit(airquality[,c(2,3)]))

## [1] 146   2

cor(na.omit(airquality[,c(2,3)]))

##             Solar.R        Wind
## Solar.R  1.00000000 -0.05679167
## Wind    -0.05679167  1.00000000

Mean imputation (MCAR)

bd<-airquality
m1<-mean(bd$Ozone,na.rm=T)
bd$Ozone[is.na(bd$Ozone)]<-m1
mean(bd$Ozone)

## [1] 42.12931

par(mfrow=c(1,2))
hist(airquality$Ozone)
hist(bd$Ozone)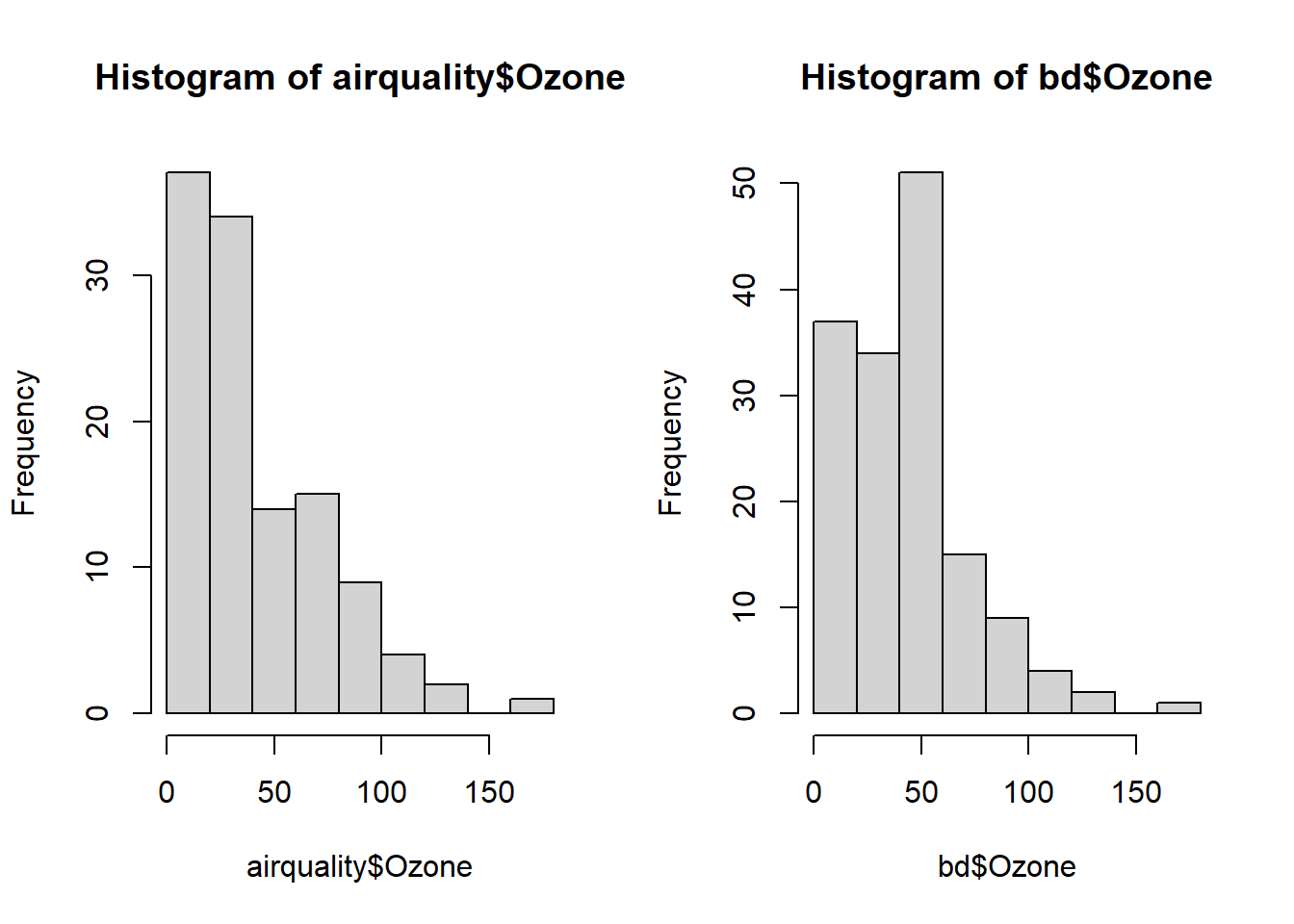

par(mfrow=c(1,2))
plot(density(airquality$Ozone,na.rm=T))
plot(density(bd$Ozone,na.rm=T))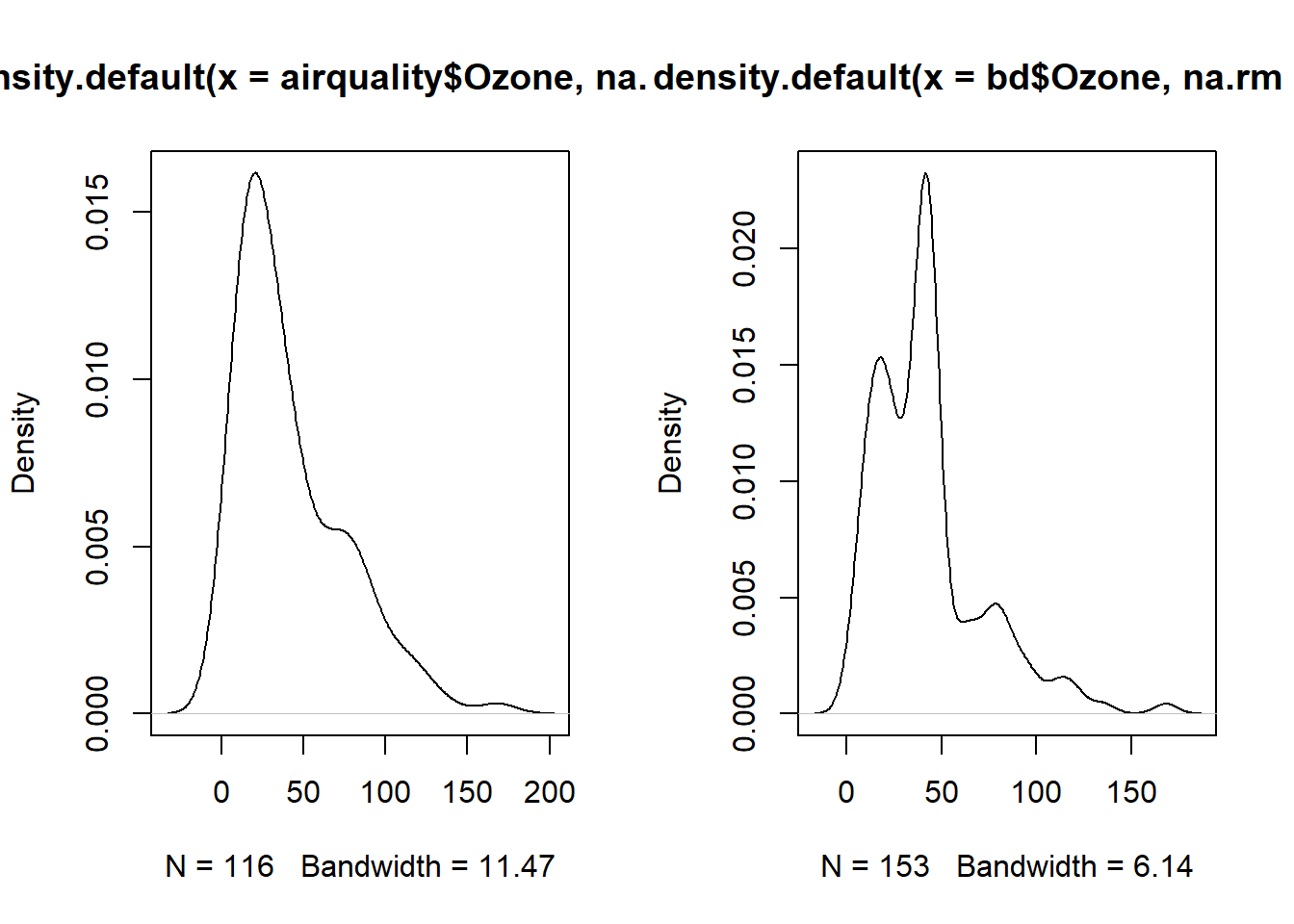

library(mice)
imp <- mice(airquality, method = "mean", m = 1, maxit = 1)

## 
##  iter imp variable
##   1   1  Ozone  Solar.R

bdi<-complete(imp)

cor(na.omit(airquality[,1:2]))

##             Ozone   Solar.R
## Ozone   1.0000000 0.3483417
## Solar.R 0.3483417 1.0000000

cor(bd[,1:2])

##         Ozone Solar.R
## Ozone       1      NA
## Solar.R    NA       1

plot(airquality$Ozone,airquality$Solar.R)
plot(bdi$Ozone,bdi$Solar.R)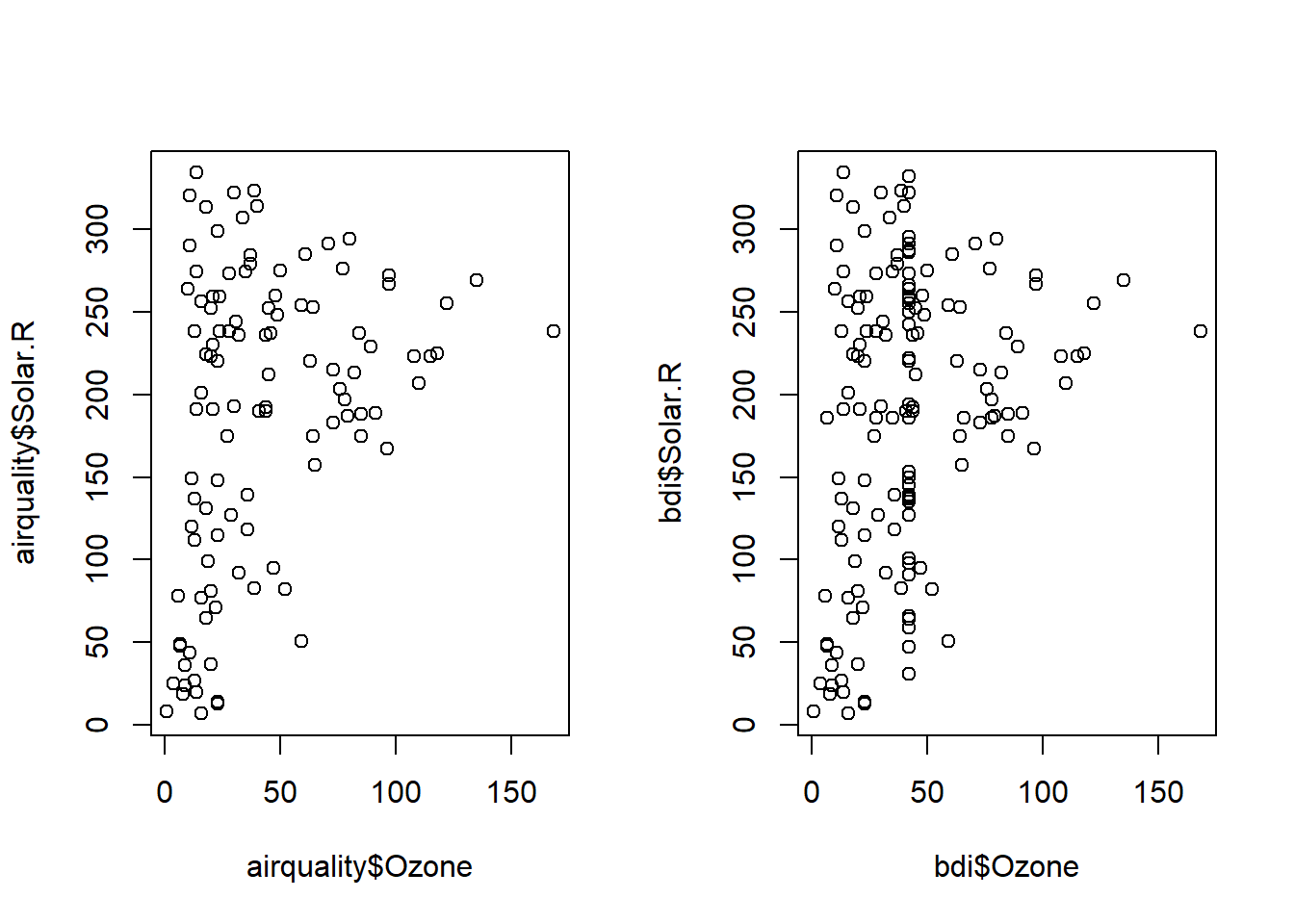

Regression imputation (MAR)

\[y_i=\beta_0+\beta_1 x_i+\epsilon_i\]

\[E[y/x]=\beta_0+\beta_1 x\]

fit <- lm(Ozone ~ Solar.R, data = airquality)
summary(fit)

## 
## Call:
## lm(formula = Ozone ~ Solar.R, data = airquality)
## 
## Residuals:
##     Min      1Q  Median      3Q 
## -48.292 -21.361  -8.864  16.373 
##     Max 
## 119.136 
## 
## Coefficients:
##             Estimate Std. Error
## (Intercept) 18.59873    6.74790
## Solar.R      0.12717    0.03278
##             t value Pr(>|t|)    
## (Intercept)   2.756 0.006856 ** 
## Solar.R       3.880 0.000179 ***
## ---
## Signif. codes:  
##   0 '***' 0.001 '**' 0.01 '*'
##   0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 31.33 on 109 degrees of freedom
##   (42 observations deleted due to missingness)
## Multiple R-squared:  0.1213, Adjusted R-squared:  0.1133 
## F-statistic: 15.05 on 1 and 109 DF,  p-value: 0.0001793

pred <- predict(fit, newdata = ic(airquality))

#para el caso 10

18.599+0.127*194

## [1] 43.237

data <- airquality[, c("Ozone", "Solar.R")]

imp <- mice(data, method = "norm.predict", seed = 1,
           m = 1, print = FALSE)

complete(imp)

##         Ozone  Solar.R
## 1    41.00000 190.0000
## 2    36.00000 118.0000
## 3    12.00000 149.0000
## 4    18.00000 313.0000
## 5    42.27981 185.9649
## 6    28.00000 168.9457
## 7    23.00000 299.0000
## 8    19.00000  99.0000
## 9     8.00000  19.0000
## 10   43.32279 194.0000
## 11    7.00000 143.9171
## 12   16.00000 256.0000
## 13   11.00000 290.0000
## 14   14.00000 274.0000
## 15   18.00000  65.0000
## 16   14.00000 334.0000
## 17   34.00000 307.0000
## 18    6.00000  78.0000
## 19   30.00000 322.0000
## 20   11.00000  44.0000
## 21    1.00000   8.0000
## 22   11.00000 320.0000
## 23    4.00000  25.0000
## 24   32.00000  92.0000
## 25   26.57468  66.0000
## 26   52.74360 266.0000
## 27   42.27706 185.9617
## 28   23.00000  13.0000
## 29   45.00000 252.0000
## 30  115.00000 223.0000
## 31   37.00000 279.0000
## 32   55.36049 286.0000
## 33   55.49133 287.0000
## 34   49.60333 242.0000
## 35   42.27603 186.0000
## 36   46.72475 220.0000
## 37   52.48191 264.0000
## 38   29.00000 127.0000
## 39   53.65951 273.0000
## 40   71.00000 291.0000
## 41   39.00000 323.0000
## 42   51.82769 259.0000
## 43   50.65008 250.0000
## 44   23.00000 148.0000
## 45   61.37934 332.0000
## 46   60.07089 322.0000
## 47   21.00000 191.0000
## 48   37.00000 284.0000
## 49   20.00000  37.0000
## 50   12.00000 120.0000
## 51   13.00000 137.0000
## 52   37.56563 150.0000
## 53   25.65877  59.0000
## 54   29.84580  91.0000
## 55   50.65008 250.0000
## 56   35.60296 135.0000
## 57   34.55620 127.0000
## 58   24.08864  47.0000
## 59   30.76171  98.0000
## 60   21.99512  31.0000
## 61   35.99549 138.0000
## 62  135.00000 269.0000
## 63   49.00000 248.0000
## 64   32.00000 236.0000
## 65   31.15424 101.0000
## 66   64.00000 175.0000
## 67   40.00000 314.0000
## 68   77.00000 276.0000
## 69   97.00000 267.0000
## 70   97.00000 272.0000
## 71   85.00000 175.0000
## 72   36.12634 139.0000
## 73   10.00000 264.0000
## 74   27.00000 175.0000
## 75   56.01471 291.0000
## 76    7.00000  48.0000
## 77   48.00000 260.0000
## 78   35.00000 274.0000
## 79   61.00000 285.0000
## 80   79.00000 187.0000
## 81   63.00000 220.0000
## 82   16.00000   7.0000
## 83   51.69684 258.0000
## 84   56.53809 295.0000
## 85   80.00000 294.0000
## 86  108.00000 223.0000
## 87   20.00000  81.0000
## 88   52.00000  82.0000
## 89   82.00000 213.0000
## 90   50.00000 275.0000
## 91   64.00000 253.0000
## 92   59.00000 254.0000
## 93   39.00000  83.0000
## 94    9.00000  24.0000
## 95   16.00000  77.0000
## 96   78.00000 228.5377
## 97   35.00000 177.2886
## 98   66.00000 214.2356
## 99  122.00000 255.0000
## 100  89.00000 229.0000
## 101 110.00000 207.0000
## 102  46.98644 222.0000
## 103  35.86465 137.0000
## 104  44.00000 192.0000
## 105  28.00000 273.0000
## 106  65.00000 157.0000
## 107  26.31299  64.0000
## 108  22.00000  71.0000
## 109  59.00000  51.0000
## 110  23.00000 115.0000
## 111  31.00000 244.0000
## 112  44.00000 190.0000
## 113  21.00000 259.0000
## 114   9.00000  36.0000
## 115  51.30431 255.0000
## 116  45.00000 212.0000
## 117 168.00000 238.0000
## 118  73.00000 215.0000
## 119  37.95816 153.0000
## 120  76.00000 203.0000
## 121 118.00000 225.0000
## 122  84.00000 237.0000
## 123  85.00000 188.0000
## 124  96.00000 167.0000
## 125  78.00000 197.0000
## 126  73.00000 183.0000
## 127  91.00000 189.0000
## 128  47.00000  95.0000
## 129  32.00000  92.0000
## 130  20.00000 252.0000
## 131  23.00000 220.0000
## 132  21.00000 230.0000
## 133  24.00000 259.0000
## 134  44.00000 236.0000
## 135  21.00000 259.0000
## 136  28.00000 238.0000
## 137   9.00000  24.0000
## 138  13.00000 112.0000
## 139  46.00000 237.0000
## 140  18.00000 224.0000
## 141  13.00000  27.0000
## 142  24.00000 238.0000
## 143  16.00000 201.0000
## 144  13.00000 238.0000
## 145  23.00000  14.0000
## 146  36.00000 139.0000
## 147   7.00000  49.0000
## 148  14.00000  20.0000
## 149  30.00000 193.0000
## 150  36.91140 145.0000
## 151  14.00000 191.0000
## 152  18.00000 131.0000
## 153  20.00000 223.0000

plot(airquality[,1:2])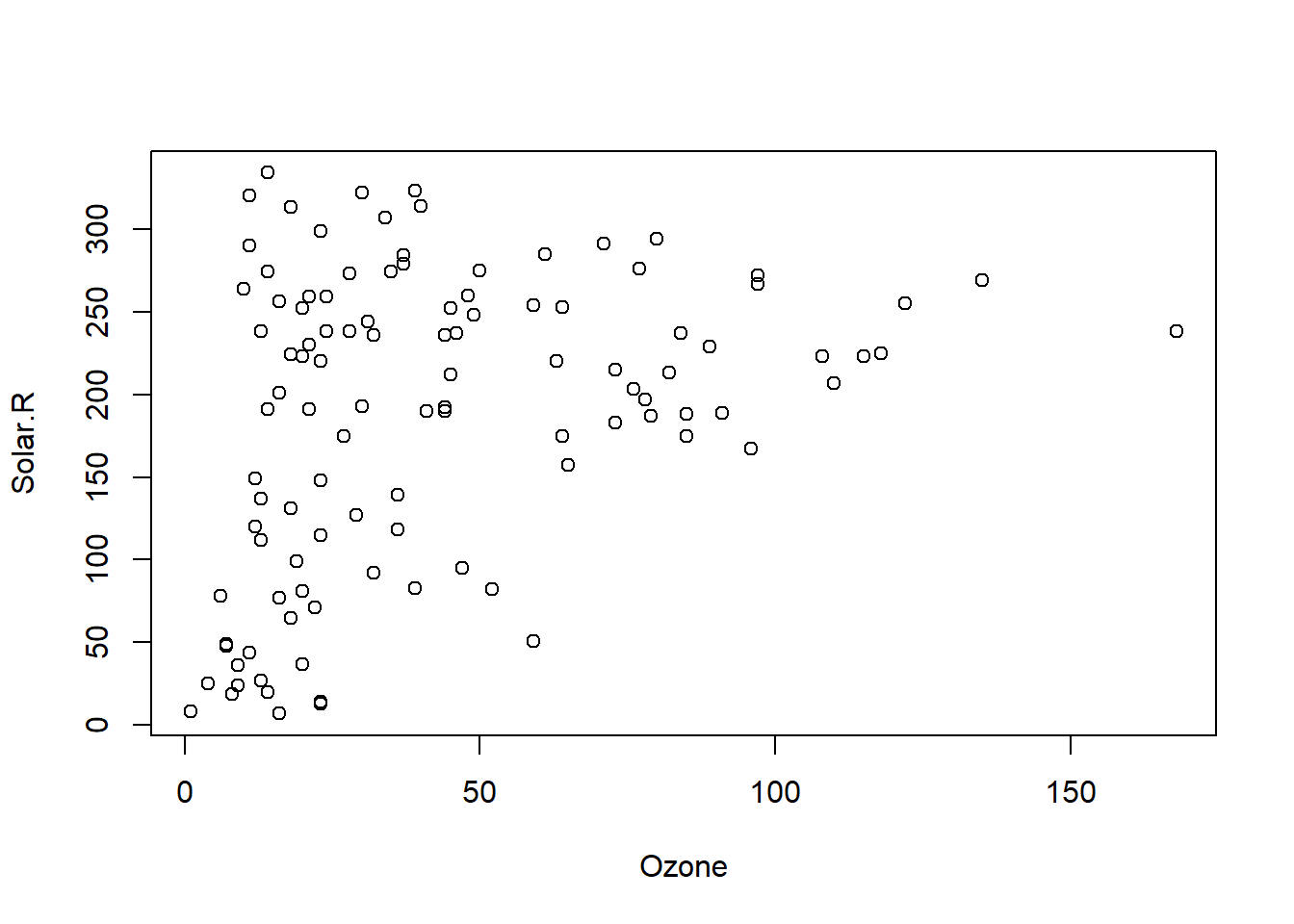

plot(complete(imp)[,1:2])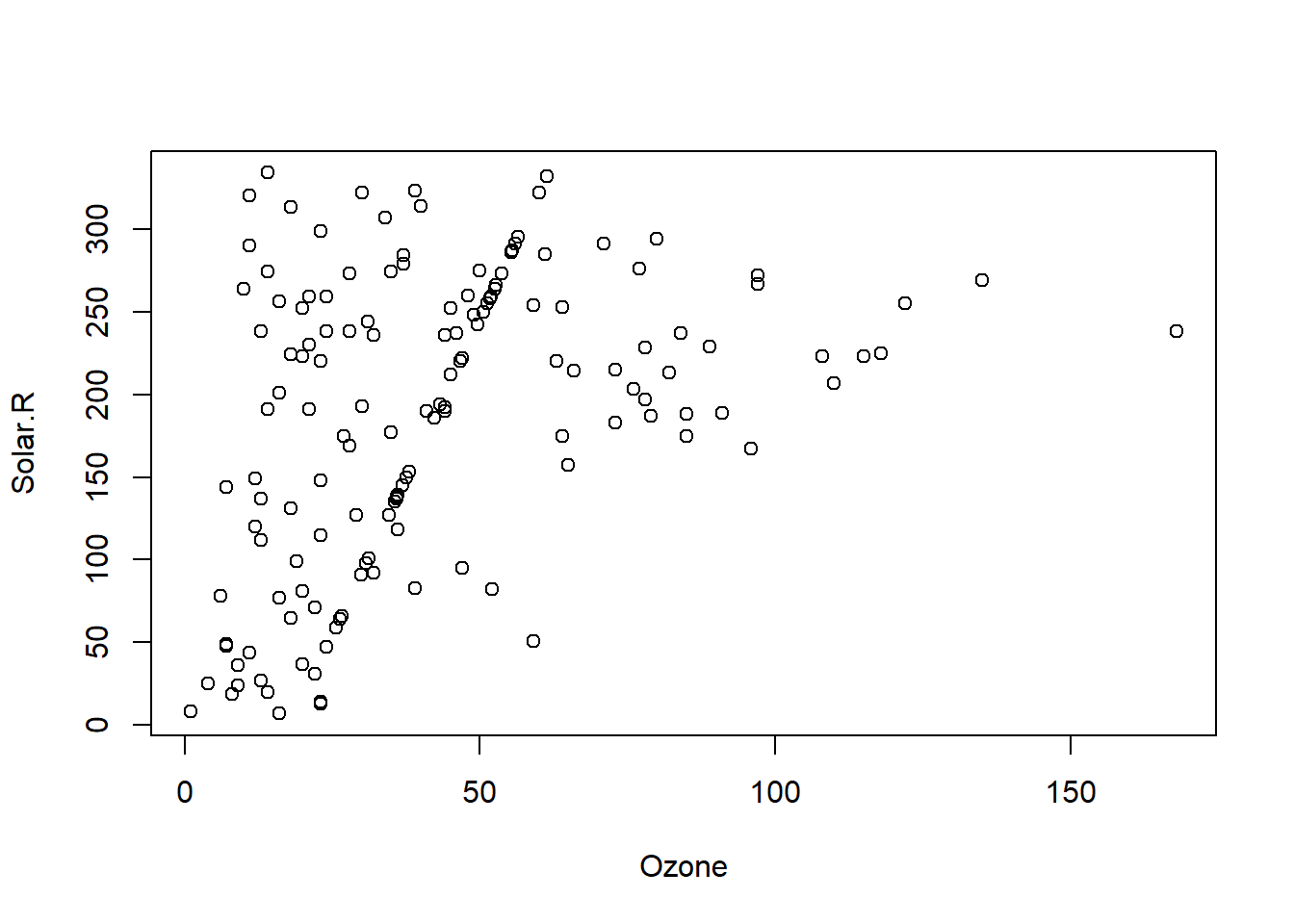

cor(na.omit(airquality[,1:2]))

##             Ozone   Solar.R
## Ozone   1.0000000 0.3483417
## Solar.R 0.3483417 1.0000000

cor(complete(imp)[,1:2])

##             Ozone   Solar.R
## Ozone   1.0000000 0.3948995
## Solar.R 0.3948995 1.0000000

Stochastic regression imputation (MAR)

\[y_i=\hat{\beta_0}+\hat{\beta_1} x_i+\hat{\epsilon_i}\]

data <- airquality[, c("Ozone", "Solar.R")]
imp <- mice(data, method = "norm.nob", m = 1, maxit = 1,
            seed = 1, print = FALSE)
complete(imp)

##           Ozone   Solar.R
## 1    41.0000000 190.00000
## 2    36.0000000 118.00000
## 3    12.0000000 149.00000
## 4    18.0000000 313.00000
## 5    93.1901074 230.44150
## 6    28.0000000 103.66507
## 7    23.0000000 299.00000
## 8    19.0000000  99.00000
## 9     8.0000000  19.00000
## 10   21.8114143 194.00000
## 11    7.0000000 169.74746
## 12   16.0000000 256.00000
## 13   11.0000000 290.00000
## 14   14.0000000 274.00000
## 15   18.0000000  65.00000
## 16   14.0000000 334.00000
## 17   34.0000000 307.00000
## 18    6.0000000  78.00000
## 19   30.0000000 322.00000
## 20   11.0000000  44.00000
## 21    1.0000000   8.00000
## 22   11.0000000 320.00000
## 23    4.0000000  25.00000
## 24   32.0000000  92.00000
## 25  -12.5439113  66.00000
## 26   53.7714213 266.00000
## 27   47.1516807  72.91707
## 28   23.0000000  13.00000
## 29   45.0000000 252.00000
## 30  115.0000000 223.00000
## 31   37.0000000 279.00000
## 32   37.7852286 286.00000
## 33   41.3376364 287.00000
## 34   29.0262061 242.00000
## 35   65.1911154 186.00000
## 36   82.6871079 220.00000
## 37   83.1114195 264.00000
## 38   29.0000000 127.00000
## 39   39.7307790 273.00000
## 40   71.0000000 291.00000
## 41   39.0000000 323.00000
## 42   90.1979525 259.00000
## 43   41.5950585 250.00000
## 44   23.0000000 148.00000
## 45  115.4565706 332.00000
## 46   76.7599696 322.00000
## 47   21.0000000 191.00000
## 48   37.0000000 284.00000
## 49   20.0000000  37.00000
## 50   12.0000000 120.00000
## 51   13.0000000 137.00000
## 52   23.8411395 150.00000
## 53    0.7555855  59.00000
## 54   -5.7687193  91.00000
## 55   16.9902402 250.00000
## 56  -12.7755115 135.00000
## 57   71.3683543 127.00000
## 58   51.3526593  47.00000
## 59   24.4868657  98.00000
## 60   31.6708004  31.00000
## 61   24.7428741 138.00000
## 62  135.0000000 269.00000
## 63   49.0000000 248.00000
## 64   32.0000000 236.00000
## 65  108.3710476 101.00000
## 66   64.0000000 175.00000
## 67   40.0000000 314.00000
## 68   77.0000000 276.00000
## 69   97.0000000 267.00000
## 70   97.0000000 272.00000
## 71   85.0000000 175.00000
## 72   11.7652825 139.00000
## 73   10.0000000 264.00000
## 74   27.0000000 175.00000
## 75   53.6734104 291.00000
## 76    7.0000000  48.00000
## 77   48.0000000 260.00000
## 78   35.0000000 274.00000
## 79   61.0000000 285.00000
## 80   79.0000000 187.00000
## 81   63.0000000 220.00000
## 82   16.0000000   7.00000
## 83   59.1510109 258.00000
## 84   75.2311817 295.00000
## 85   80.0000000 294.00000
## 86  108.0000000 223.00000
## 87   20.0000000  81.00000
## 88   52.0000000  82.00000
## 89   82.0000000 213.00000
## 90   50.0000000 275.00000
## 91   64.0000000 253.00000
## 92   59.0000000 254.00000
## 93   39.0000000  83.00000
## 94    9.0000000  24.00000
## 95   16.0000000  77.00000
## 96   78.0000000 254.64941
## 97   35.0000000 199.67614
## 98   66.0000000 216.97628
## 99  122.0000000 255.00000
## 100  89.0000000 229.00000
## 101 110.0000000 207.00000
## 102  41.4834780 222.00000
## 103 -33.1867993 137.00000
## 104  44.0000000 192.00000
## 105  28.0000000 273.00000
## 106  65.0000000 157.00000
## 107 -12.1337321  64.00000
## 108  22.0000000  71.00000
## 109  59.0000000  51.00000
## 110  23.0000000 115.00000
## 111  31.0000000 244.00000
## 112  44.0000000 190.00000
## 113  21.0000000 259.00000
## 114   9.0000000  36.00000
## 115  62.1793726 255.00000
## 116  45.0000000 212.00000
## 117 168.0000000 238.00000
## 118  73.0000000 215.00000
## 119  38.0347443 153.00000
## 120  76.0000000 203.00000
## 121 118.0000000 225.00000
## 122  84.0000000 237.00000
## 123  85.0000000 188.00000
## 124  96.0000000 167.00000
## 125  78.0000000 197.00000
## 126  73.0000000 183.00000
## 127  91.0000000 189.00000
## 128  47.0000000  95.00000
## 129  32.0000000  92.00000
## 130  20.0000000 252.00000
## 131  23.0000000 220.00000
## 132  21.0000000 230.00000
## 133  24.0000000 259.00000
## 134  44.0000000 236.00000
## 135  21.0000000 259.00000
## 136  28.0000000 238.00000
## 137   9.0000000  24.00000
## 138  13.0000000 112.00000
## 139  46.0000000 237.00000
## 140  18.0000000 224.00000
## 141  13.0000000  27.00000
## 142  24.0000000 238.00000
## 143  16.0000000 201.00000
## 144  13.0000000 238.00000
## 145  23.0000000  14.00000
## 146  36.0000000 139.00000
## 147   7.0000000  49.00000
## 148  14.0000000  20.00000
## 149  30.0000000 193.00000
## 150   7.9575138 145.00000
## 151  14.0000000 191.00000
## 152  18.0000000 131.00000
## 153  20.0000000 223.00000

plot(airquality[,1:2])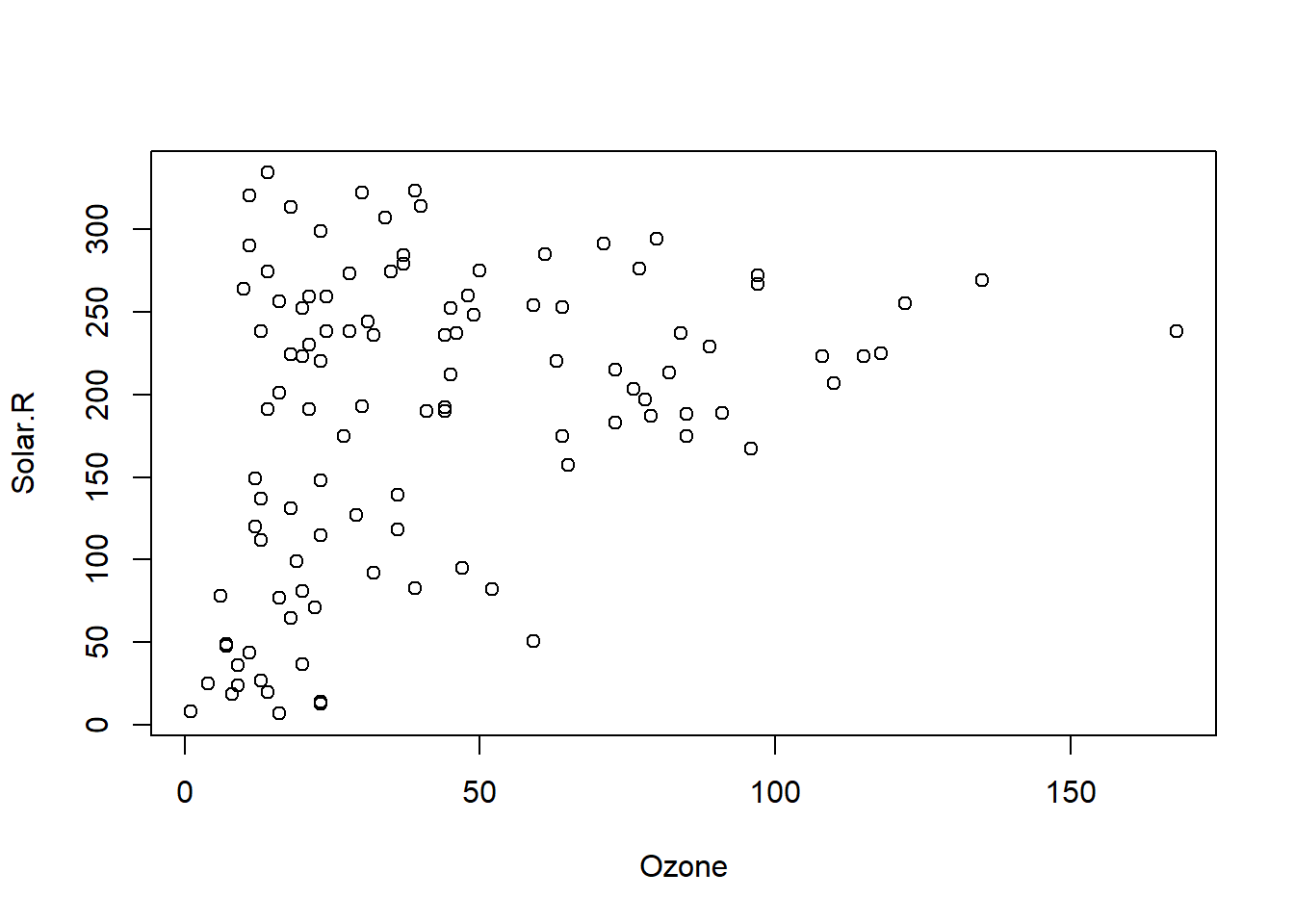

plot(complete(imp)[,1:2])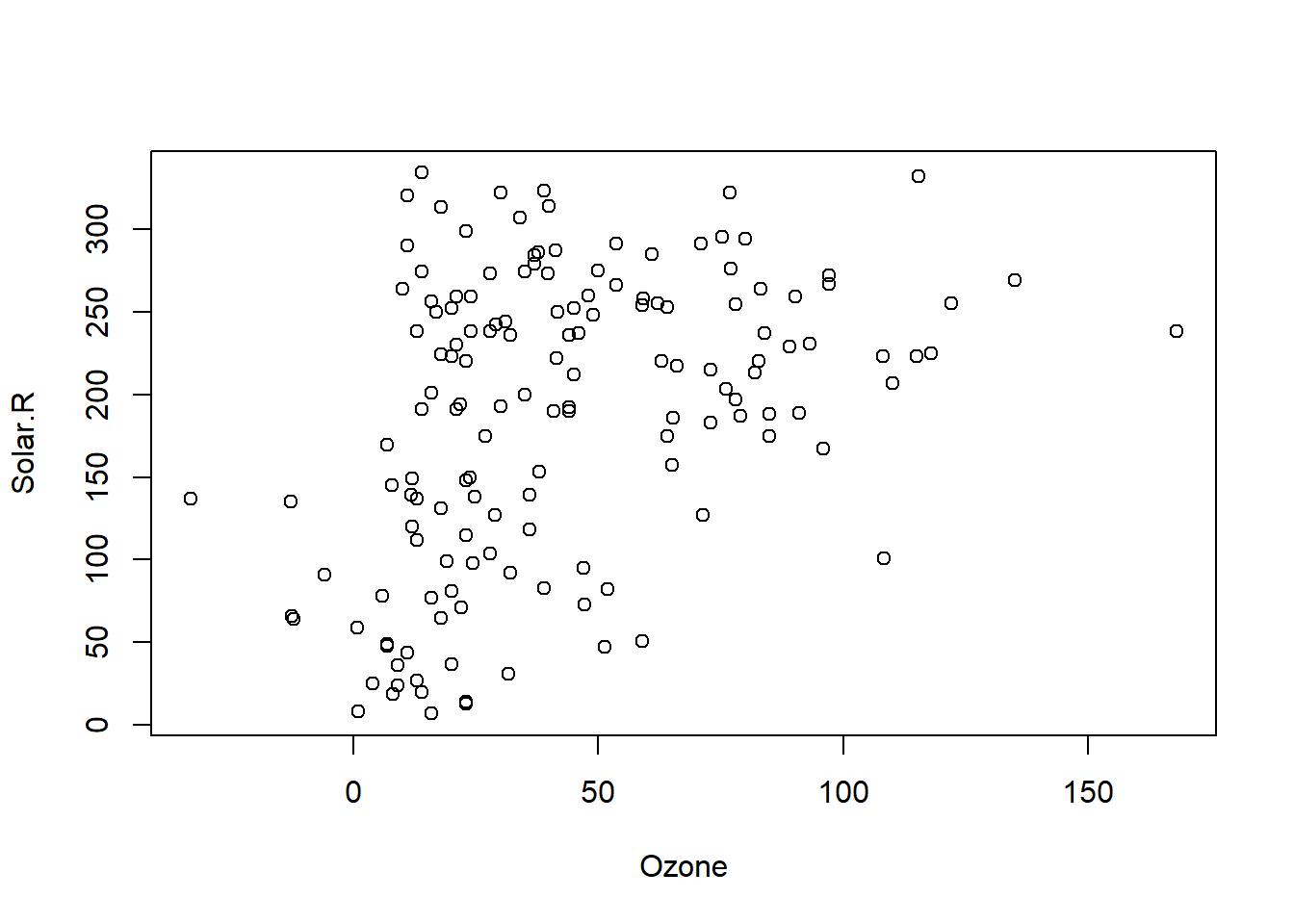

cor(na.omit(airquality[,1:2]))

##             Ozone   Solar.R
## Ozone   1.0000000 0.3483417
## Solar.R 0.3483417 1.0000000

cor(complete(imp)[,1:2])

##             Ozone   Solar.R
## Ozone   1.0000000 0.3964026
## Solar.R 0.3964026 1.0000000

plot(density(airquality$Ozone,na.rm=T))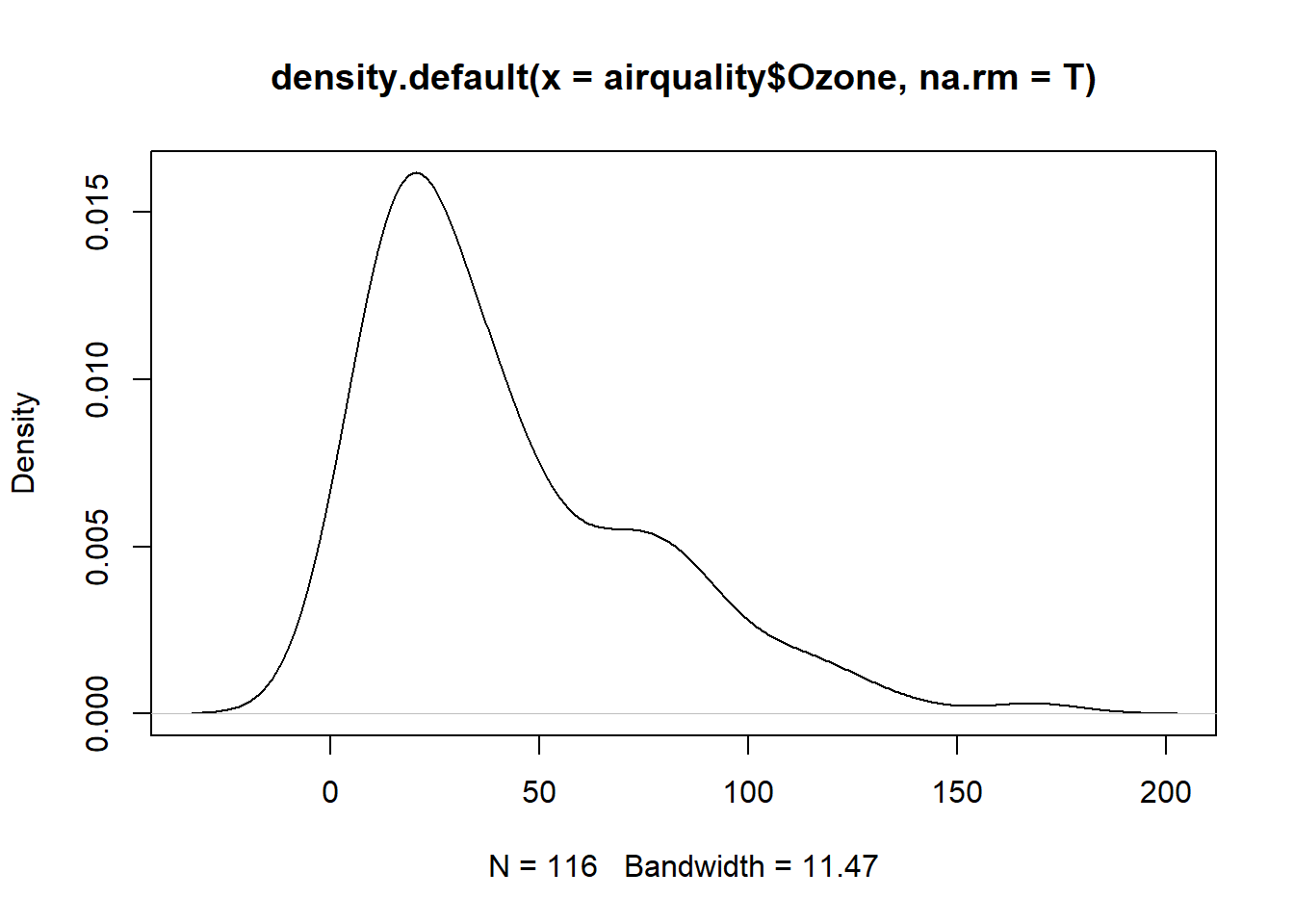

plot(density(complete(imp)[,1],na.rm=T))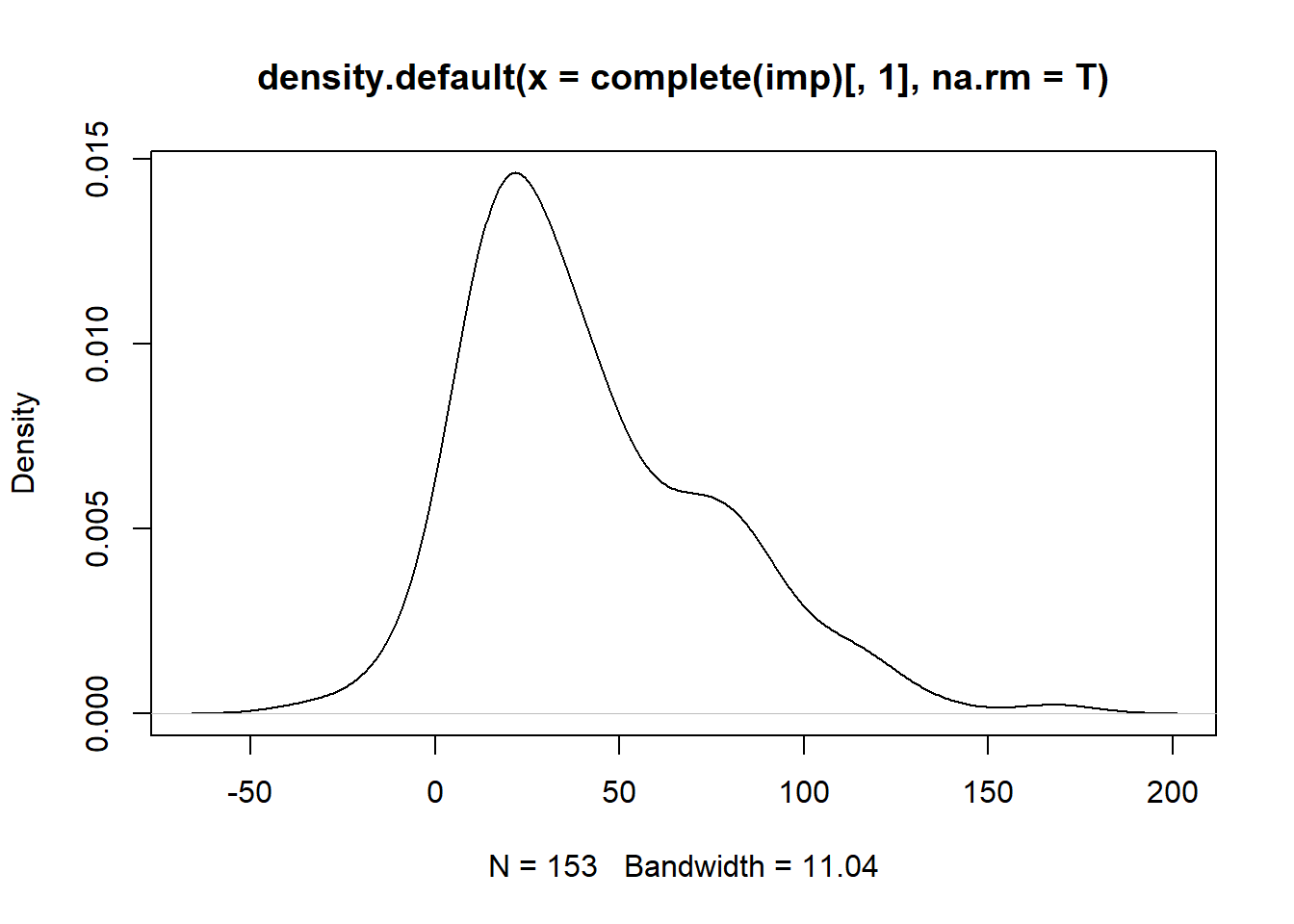

plot(density(airquality$Solar.R,na.rm=T))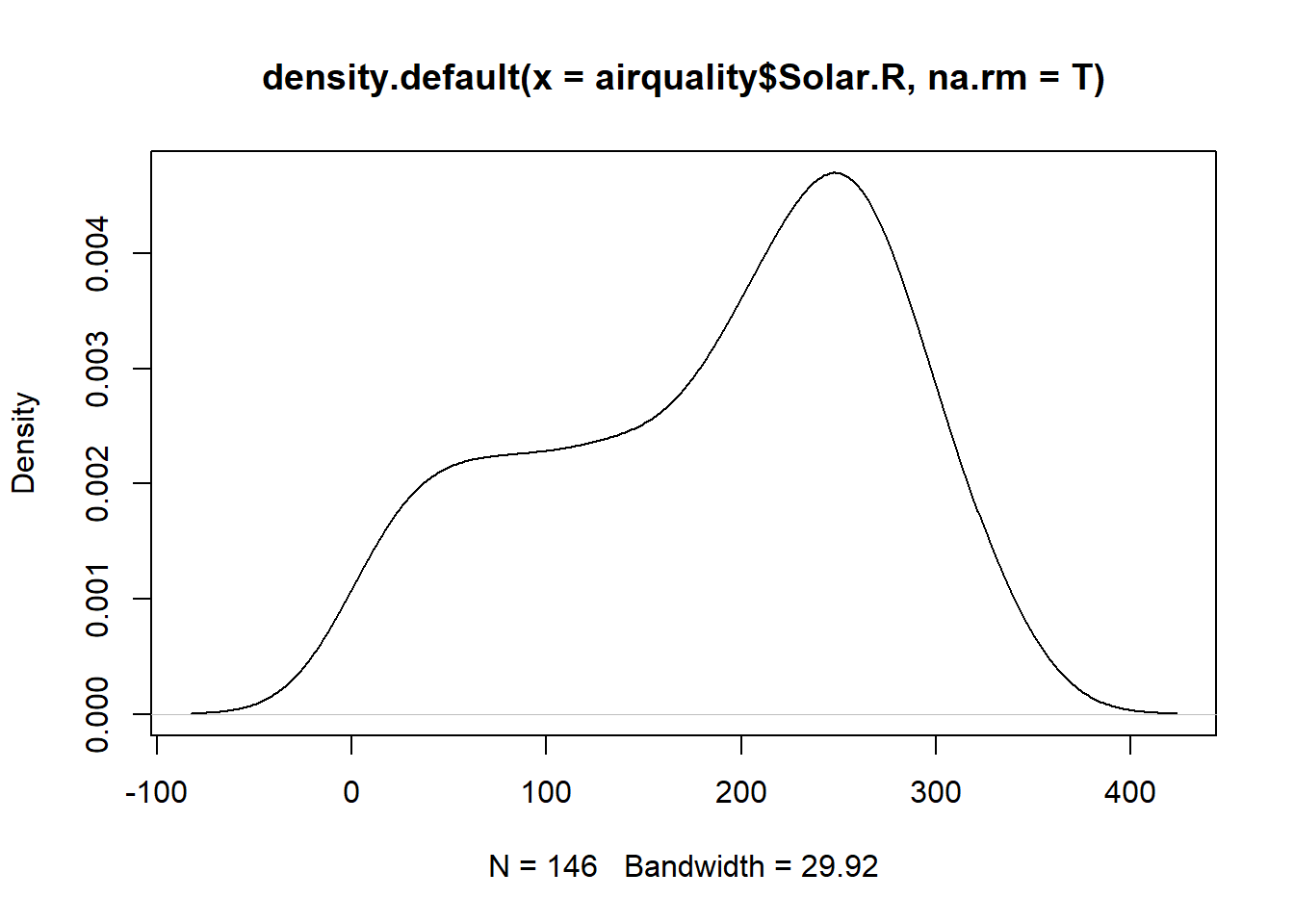

plot(density(complete(imp)[,2],na.rm=T))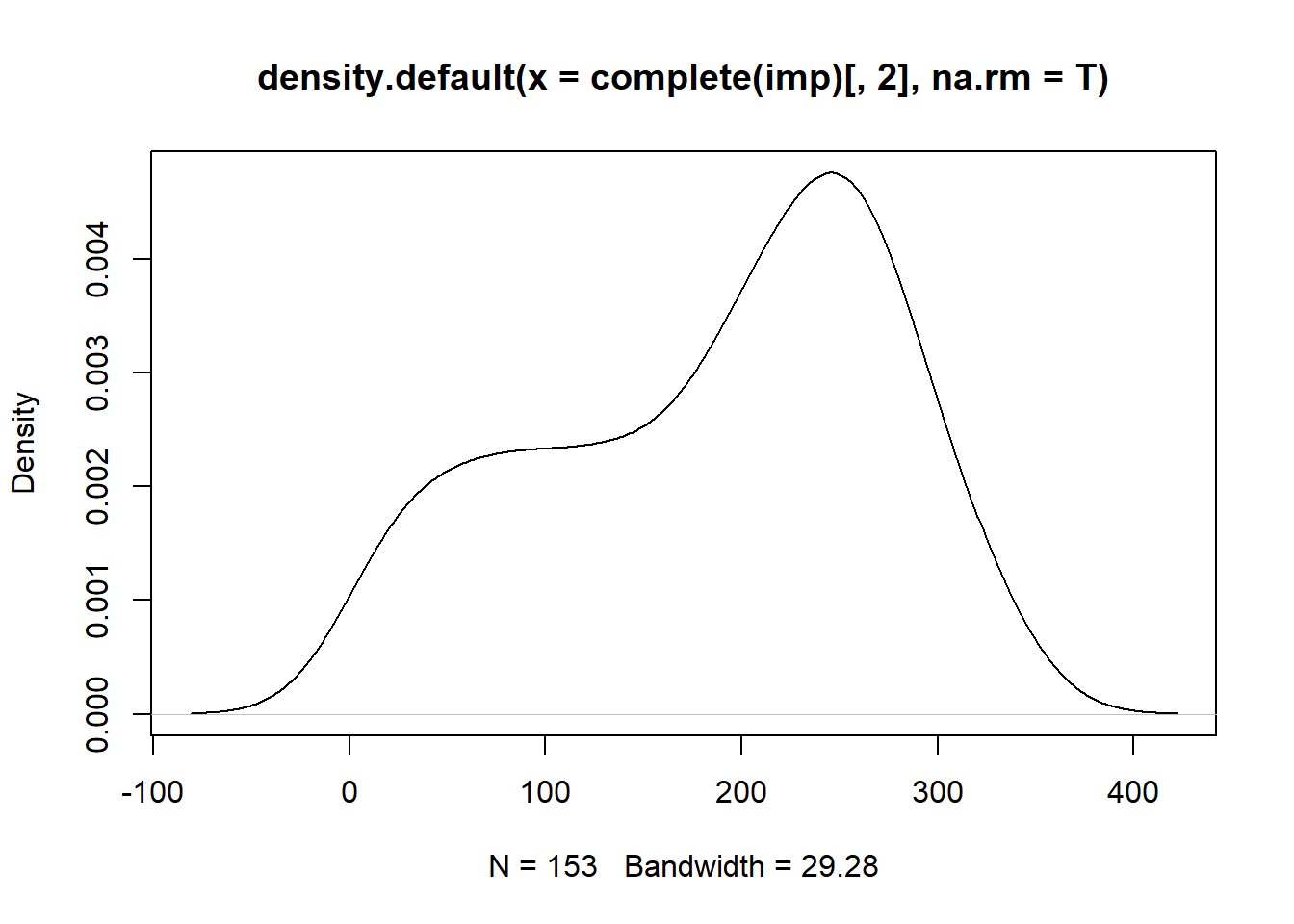

imp<-mice(airquality, method = "norm.nob", m = 1, maxit = 1,
            seed = 1, print = FALSE)
complete(imp)

##           Ozone    Solar.R Wind
## 1    41.0000000 190.000000  7.4
## 2    36.0000000 118.000000  8.0
## 3    12.0000000 149.000000 12.6
## 4    18.0000000 313.000000 11.5
## 5    20.5007386 174.406477 14.3
## 6    28.0000000 140.047720 14.9
## 7    23.0000000 299.000000  8.6
## 8    19.0000000  99.000000 13.8
## 9     8.0000000  19.000000 20.1
## 10   19.9813337 194.000000  8.6
## 11    7.0000000 175.896881  6.9
## 12   16.0000000 256.000000  9.7
## 13   11.0000000 290.000000  9.2
## 14   14.0000000 274.000000 10.9
## 15   18.0000000  65.000000 13.2
## 16   14.0000000 334.000000 11.5
## 17   34.0000000 307.000000 12.0
## 18    6.0000000  78.000000 18.4
## 19   30.0000000 322.000000 11.5
## 20   11.0000000  44.000000  9.7
## 21    1.0000000   8.000000  9.7
## 22   11.0000000 320.000000 16.6
## 23    4.0000000  25.000000  9.7
## 24   32.0000000  92.000000 12.0
## 25  -43.0343740  66.000000 16.6
## 26    3.3396801 266.000000 14.9
## 27   18.3933655   8.744525  8.0
## 28   23.0000000  13.000000 12.0
## 29   45.0000000 252.000000 14.9
## 30  115.0000000 223.000000  5.7
## 31   37.0000000 279.000000  7.4
## 32   39.7516986 286.000000  8.6
## 33   31.3839433 287.000000  9.7
## 34   -8.6316915 242.000000 16.1
## 35   71.4038792 186.000000  9.2
## 36   86.2547074 220.000000  8.6
## 37   56.3247528 264.000000 14.3
## 38   29.0000000 127.000000  9.7
## 39   65.7382192 273.000000  6.9
## 40   71.0000000 291.000000 13.8
## 41   39.0000000 323.000000 11.5
## 42   99.7663357 259.000000 10.9
## 43   71.0135556 250.000000  9.2
## 44   23.0000000 148.000000  8.0
## 45   81.8344779 332.000000 13.8
## 46   61.6649678 322.000000 11.5
## 47   21.0000000 191.000000 14.9
## 48   37.0000000 284.000000 20.7
## 49   20.0000000  37.000000  9.2
## 50   12.0000000 120.000000 11.5
## 51   13.0000000 137.000000 10.3
## 52   45.2131440 150.000000  6.3
## 53   45.1192943  59.000000  1.7
## 54   30.9805688  91.000000  4.6
## 55   36.6503552 250.000000  6.3
## 56   12.9901939 135.000000  8.0
## 57   75.8450620 127.000000  8.0
## 58   48.2955351  47.000000 10.3
## 59   38.4690813  98.000000 11.5
## 60   29.1923696  31.000000 14.9
## 61   54.6909678 138.000000  8.0
## 62  135.0000000 269.000000  4.1
## 63   49.0000000 248.000000  9.2
## 64   32.0000000 236.000000  9.2
## 65   94.7972277 101.000000 10.9
## 66   64.0000000 175.000000  4.6
## 67   40.0000000 314.000000 10.9
## 68   77.0000000 276.000000  5.1
## 69   97.0000000 267.000000  6.3
## 70   97.0000000 272.000000  5.7
## 71   85.0000000 175.000000  7.4
## 72   34.0203036 139.000000  8.6
## 73   10.0000000 264.000000 14.3
## 74   27.0000000 175.000000 14.9
## 75   55.9305086 291.000000 14.9
## 76    7.0000000  48.000000 14.3
## 77   48.0000000 260.000000  6.9
## 78   35.0000000 274.000000 10.3
## 79   61.0000000 285.000000  6.3
## 80   79.0000000 187.000000  5.1
## 81   63.0000000 220.000000 11.5
## 82   16.0000000   7.000000  6.9
## 83   60.2221568 258.000000  9.7
## 84   66.5040195 295.000000 11.5
## 85   80.0000000 294.000000  8.6
## 86  108.0000000 223.000000  8.0
## 87   20.0000000  81.000000  8.6
## 88   52.0000000  82.000000 12.0
## 89   82.0000000 213.000000  7.4
## 90   50.0000000 275.000000  7.4
## 91   64.0000000 253.000000  7.4
## 92   59.0000000 254.000000  9.2
## 93   39.0000000  83.000000  6.9
## 94    9.0000000  24.000000 13.8
## 95   16.0000000  77.000000  7.4
## 96   78.0000000 252.798784  6.9
## 97   35.0000000 201.411206  7.4
## 98   66.0000000 204.435959  4.6
## 99  122.0000000 255.000000  4.0
## 100  89.0000000 229.000000 10.3
## 101 110.0000000 207.000000  8.0
## 102  67.4342874 222.000000  8.6
## 103  -0.5541087 137.000000 11.5
## 104  44.0000000 192.000000 11.5
## 105  28.0000000 273.000000 11.5
## 106  65.0000000 157.000000  9.7
## 107   3.6275851  64.000000 11.5
## 108  22.0000000  71.000000 10.3
## 109  59.0000000  51.000000  6.3
## 110  23.0000000 115.000000  7.4
## 111  31.0000000 244.000000 10.9
## 112  44.0000000 190.000000 10.3
## 113  21.0000000 259.000000 15.5
## 114   9.0000000  36.000000 14.3
## 115  39.3715767 255.000000 12.6
## 116  45.0000000 212.000000  9.7
## 117 168.0000000 238.000000  3.4
## 118  73.0000000 215.000000  8.0
## 119  73.3973647 153.000000  5.7
## 120  76.0000000 203.000000  9.7
## 121 118.0000000 225.000000  2.3
## 122  84.0000000 237.000000  6.3
## 123  85.0000000 188.000000  6.3
## 124  96.0000000 167.000000  6.9
## 125  78.0000000 197.000000  5.1
## 126  73.0000000 183.000000  2.8
## 127  91.0000000 189.000000  4.6
## 128  47.0000000  95.000000  7.4
## 129  32.0000000  92.000000 15.5
## 130  20.0000000 252.000000 10.9
## 131  23.0000000 220.000000 10.3
## 132  21.0000000 230.000000 10.9
## 133  24.0000000 259.000000  9.7
## 134  44.0000000 236.000000 14.9
## 135  21.0000000 259.000000 15.5
## 136  28.0000000 238.000000  6.3
## 137   9.0000000  24.000000 10.9
## 138  13.0000000 112.000000 11.5
## 139  46.0000000 237.000000  6.9
## 140  18.0000000 224.000000 13.8
## 141  13.0000000  27.000000 10.3
## 142  24.0000000 238.000000 10.3
## 143  16.0000000 201.000000  8.0
## 144  13.0000000 238.000000 12.6
## 145  23.0000000  14.000000  9.2
## 146  36.0000000 139.000000 10.3
## 147   7.0000000  49.000000 10.3
## 148  14.0000000  20.000000 16.6
## 149  30.0000000 193.000000  6.9
## 150   6.2345801 145.000000 13.2
## 151  14.0000000 191.000000 14.3
## 152  18.0000000 131.000000  8.0
## 153  20.0000000 223.000000 11.5
##     Temp Month Day
## 1     67     5   1
## 2     72     5   2
## 3     74     5   3
## 4     62     5   4
## 5     56     5   5
## 6     66     5   6
## 7     65     5   7
## 8     59     5   8
## 9     61     5   9
## 10    69     5  10
## 11    74     5  11
## 12    69     5  12
## 13    66     5  13
## 14    68     5  14
## 15    58     5  15
## 16    64     5  16
## 17    66     5  17
## 18    57     5  18
## 19    68     5  19
## 20    62     5  20
## 21    59     5  21
## 22    73     5  22
## 23    61     5  23
## 24    61     5  24
## 25    57     5  25
## 26    58     5  26
## 27    57     5  27
## 28    67     5  28
## 29    81     5  29
## 30    79     5  30
## 31    76     5  31
## 32    78     6   1
## 33    74     6   2
## 34    67     6   3
## 35    84     6   4
## 36    85     6   5
## 37    79     6   6
## 38    82     6   7
## 39    87     6   8
## 40    90     6   9
## 41    87     6  10
## 42    93     6  11
## 43    92     6  12
## 44    82     6  13
## 45    80     6  14
## 46    79     6  15
## 47    77     6  16
## 48    72     6  17
## 49    65     6  18
## 50    73     6  19
## 51    76     6  20
## 52    77     6  21
## 53    76     6  22
## 54    76     6  23
## 55    76     6  24
## 56    75     6  25
## 57    78     6  26
## 58    73     6  27
## 59    80     6  28
## 60    77     6  29
## 61    83     6  30
## 62    84     7   1
## 63    85     7   2
## 64    81     7   3
## 65    84     7   4
## 66    83     7   5
## 67    83     7   6
## 68    88     7   7
## 69    92     7   8
## 70    92     7   9
## 71    89     7  10
## 72    82     7  11
## 73    73     7  12
## 74    81     7  13
## 75    91     7  14
## 76    80     7  15
## 77    81     7  16
## 78    82     7  17
## 79    84     7  18
## 80    87     7  19
## 81    85     7  20
## 82    74     7  21
## 83    81     7  22
## 84    82     7  23
## 85    86     7  24
## 86    85     7  25
## 87    82     7  26
## 88    86     7  27
## 89    88     7  28
## 90    86     7  29
## 91    83     7  30
## 92    81     7  31
## 93    81     8   1
## 94    81     8   2
## 95    82     8   3
## 96    86     8   4
## 97    85     8   5
## 98    87     8   6
## 99    89     8   7
## 100   90     8   8
## 101   90     8   9
## 102   92     8  10
## 103   86     8  11
## 104   86     8  12
## 105   82     8  13
## 106   80     8  14
## 107   79     8  15
## 108   77     8  16
## 109   79     8  17
## 110   76     8  18
## 111   78     8  19
## 112   78     8  20
## 113   77     8  21
## 114   72     8  22
## 115   75     8  23
## 116   79     8  24
## 117   81     8  25
## 118   86     8  26
## 119   88     8  27
## 120   97     8  28
## 121   94     8  29
## 122   96     8  30
## 123   94     8  31
## 124   91     9   1
## 125   92     9   2
## 126   93     9   3
## 127   93     9   4
## 128   87     9   5
## 129   84     9   6
## 130   80     9   7
## 131   78     9   8
## 132   75     9   9
## 133   73     9  10
## 134   81     9  11
## 135   76     9  12
## 136   77     9  13
## 137   71     9  14
## 138   71     9  15
## 139   78     9  16
## 140   67     9  17
## 141   76     9  18
## 142   68     9  19
## 143   82     9  20
## 144   64     9  21
## 145   71     9  22
## 146   81     9  23
## 147   69     9  24
## 148   63     9  25
## 149   70     9  26
## 150   77     9  27
## 151   75     9  28
## 152   76     9  29
## 153   68     9  30

md.pattern(airquality, plot = T)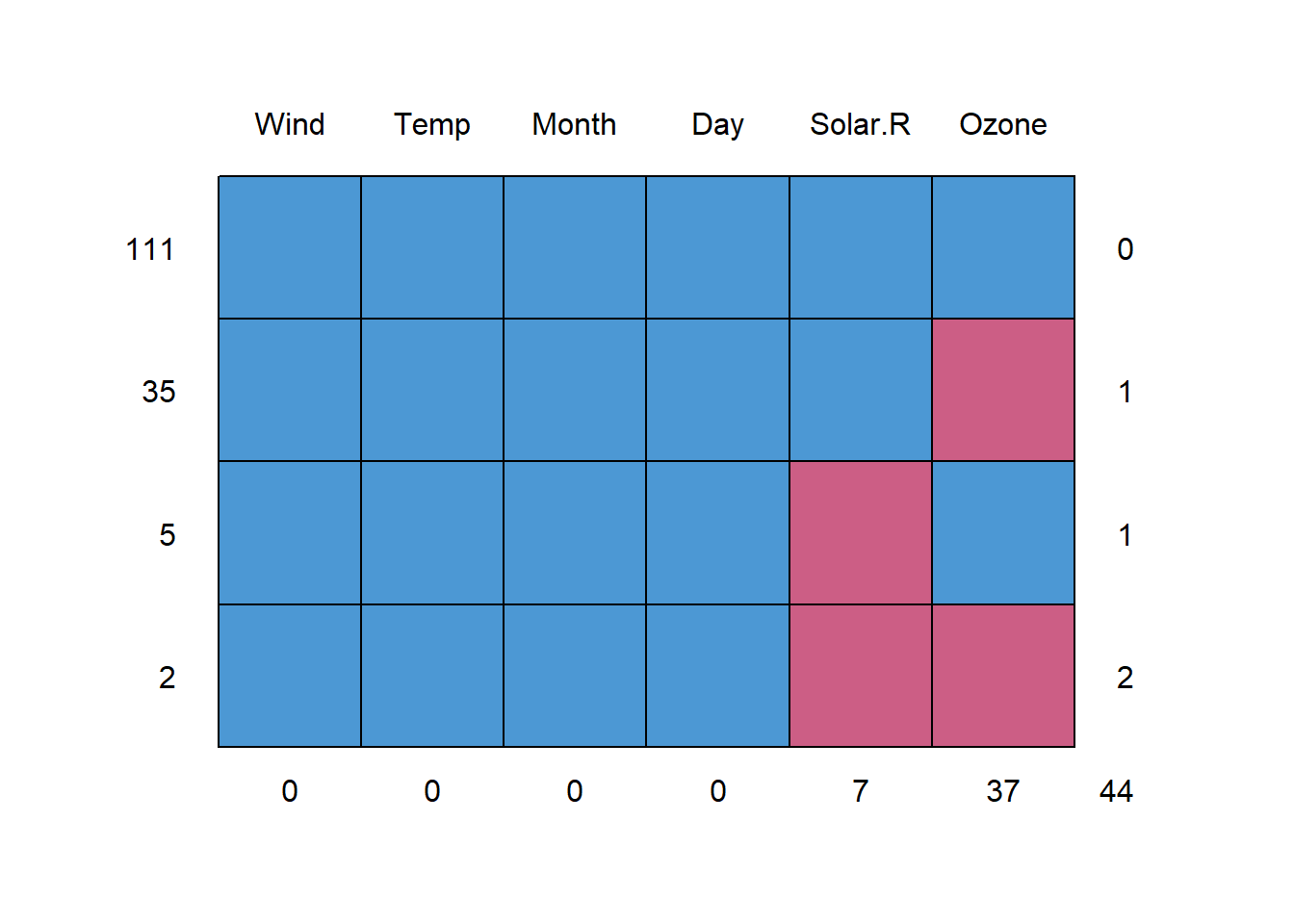

##     Wind Temp Month Day Solar.R
## 111    1    1     1   1       1
## 35     1    1     1   1       1
## 5      1    1     1   1       0
## 2      1    1     1   1       0
##        0    0     0   0       7
##     Ozone   
## 111     1  0
## 35      0  1
## 5       1  1
## 2       0  2
##        37 44

flux(airquality)[,1:3]

##              pobs     influx
## Ozone   0.7581699 0.20938215
## Solar.R 0.9542484 0.03775744
## Wind    1.0000000 0.00000000
## Temp    1.0000000 0.00000000
## Month   1.0000000 0.00000000
## Day     1.0000000 0.00000000
##           outflux
## Ozone   0.1136364
## Solar.R 0.7954545
## Wind    1.0000000
## Temp    1.0000000
## Month   1.0000000
## Day     1.0000000

Allaire, JJ, Yihui Xie, Jonathan McPherson, Javier Luraschi, Kevin Ushey, Aron Atkins, Hadley Wickham, Joe Cheng, Winston Chang, and Richard Iannone. 2020. Rmarkdown: Dynamic Documents for r. https://CRAN.R-project.org/package=rmarkdown.

R Core Team. 2019. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Ted, Kwartler. 2017. Text mining in practice with R. https://doi.org/10.1080/00949655.2019.1630887.

Xie, Yihui. 2019. Knitr: A General-Purpose Package for Dynamic Report Generation in r. https://CRAN.R-project.org/package=knitr.

———. 2020. Bookdown: Authoring Books and Technical Documents with r Markdown. https://CRAN.R-project.org/package=bookdown.

Xie, Yihui, J. J. Allaire, and Garrett Grolemund. 2018. “How to Read This Book.” Transforming Climate Finance and Green Investment with Blockchains, 1. https://doi.org/10.1016/b978-0-12-814447-3.00041-0.