4 Probabilidades

Ejercicios

  1. Sea el experimento aleatorio lanzar 2 dados y sumar el resultado, ¿cuáles son todos los posibles resultados de este experimento aleatorio?

Resp. (2,3,4,5,6,7,8,9,11,12); 9 (4,5),(5,4),(6,3),(3,6)

  1. Un estudiante va a dar su primer parcial sobre 30 puntos, el examen es de tipo falso/verdadero. El estudiante no se preparo y responderá al azar el examen, ¿cuáles son los posibles resultados del examen?

Resp. La nota del estudiante puede estar entre 0 al 30

  1. El juego del cacho es un juego donde se lanzan 5 dados.

Tarea. ¿Cuántos resultados posibles existen al lanzar 5 dados?

1 dado (6) 2 dados (1,1), (1,2), (1,3). … (6,6) 3 dados (1,1,1), (1,1,2), …. (6,6,6) 4 dados (1,1,1,1), (1,1,1,2)…. (6,6,6,6) 5 dados

4.1 Probabilidad e Inferencia estadística

  • Experimento: Proceso mediante el cual se obtiene un resultado de una observación.

  • Experimento aleatorio: Cuando los resultados de la observación no se puede predecir con exactitud antes de realizar el experimento.

  • Espacio Muestral: Es la colección (conjunto) de todos los resultados posibles de un experimento aleatorio. Denotado por

\[\Omega\]

Ejemplo, el juego del cacho es un juego donde se lanzan 5 dados. ¿Cuántos resultados posibles existen al lanzar 5 dados?

Respuesta, iniciemos observando los resultados de un dado, luego de 2, hasta llegar a 5 dados.

  • 1 dado: (1,2,3,4,5,6). \(\#\Omega=6\)

  • 2 dados: \(\#\Omega=36=6*6\)

  • 3 dados: \(\#\Omega=216\)

  • 4 dados: \(\#\Omega=1296\)

  • 5 dados: \(\#\Omega=7776\)

  • Evento: Un subconjunto del espacio muestral

4.1.1 Probabilidad

Es una medida de incertidumbre al rededor de un experimento aleatorio, esta medida se calcula en base a eventos de interés y toma valores entre 0 y 1.

Una definición formal de probabilidad es:

\[P(A)= \frac{\text{Casos posibles}}{\text{Casos totales}}=\frac{\#A}{\# \Omega}\] Ejemplos,

  • En el lanzamiento de una moneda, ¿cuál es la probabilidad de obtener cara?

\[P(cara)=\frac{1}{2}=0.5\]

  • En el lanzamiento de un dado, ¿cuál es la probabilidad de obtener un número par?

\[P(par)=\frac{3}{6}=0.5\]

  • En el lanzamiento de dos dados, ¿cuál es la probabilidad de obtener 7?

\[P(7)=\frac{6}{36}\]

  • En el juego del cacho, ¿cuál es la probabilidad de obtener dormida (todos las caras de los dados iguales)?

\[P(Dormida)=\frac{6}{7776}=0.0007716\] * ¿Cuál es la probabilidad de aprobar la materia de Estadística I para cualquier estudiante al inicio del semestre?

\[P(aprobar)=\frac{\geq 51}{NotasPosibles}=\frac{50}{101}=0.495\] ## Distribuciones muestrales

Variable aleatoria: Es una función que asigna a los eventos un número.

La idea de las distribuciones muestrales es estudiar el comportamiento de todas las muestras posibles a partir de una estadística.

Estadística: Un valor calculado a partir de la muestra

Ejemplo, imaginemos que tenemos un grupo/población de 5 estudiantes con el tiempo que normalmente demoran en llegar a la universidad desde sus casas.

  • PO: (A,B,C,D,E)
  • Y: Tiempo en minutos en llegar desde sus casas a la U

\[Y=\{Y_A=20,Y_B=30,Y_C=35,Y_D=60,Y_E=20\}=\{20,30,35,60,20\}\] ¿Cuál es el promedio del tiempo que demoran en llegar los estudiantes a la Universidad?

\[\bar{Y}=\frac{\sum_U y_i}{N}=\frac{165}{5}=33\]

Imaginemos que definimos un tamaño de muestra de \(n=2\), ¿Cuántas muestras posibles existen?, cuáles son los valores de las medias en cada muestra para la variable \(Y\).

  • (A,B), (A,C), (A,D), (A,E), (B,C), (B,D), (B,E), (C,D), (C,E), (D,E)
  • (20,30), (20,35), (20,60), (20,20), (30,35), (30,60), (30,20), (35,60), (35,20), (60,20)

\[\hat{\theta}=\{\bar{y}_1=25 ,\bar{y}_2=27.5,\bar{y}_3=40,\bar{y}_4=20,\bar{y}_5=32.5,\bar{y}_6=45,\bar{y}_7=25,\bar{y}_8=47.5,\bar{y}_9=27.5,\bar{y}_{10}=40\}\] ¿Cuál sera la media de las medias muestrales?

\[\bar{\bar{Y}}=\frac{\sum_{i=1}^{10}\bar{y}_i}{10}=33\]

Veamos el ejemplo ampliado, con una población de 20 estudiantes y una muestra de 4, para la misma variable.

  • (E1,E2,E3,E4,E5,E6,…,E20)

\[Y=\{20,25,40,60,70,10,35,45,40,20,33,50,55,50,20,25,55,65,30,35\}\] * Las muestras posibles son de 4845 * ¿Cuál es el promedio de la población?

\[\bar{Y}=\frac{783}{20}=39.15\]

y<-c(20,25,40,60,70,10,35,45,40,20,33,50,55,50,20,25,55,65,30,35)
ym<-combn(y,4)
yy<-apply(ym,2,mean)
sum(yy)/4845
## [1] 39.15
hist(yy)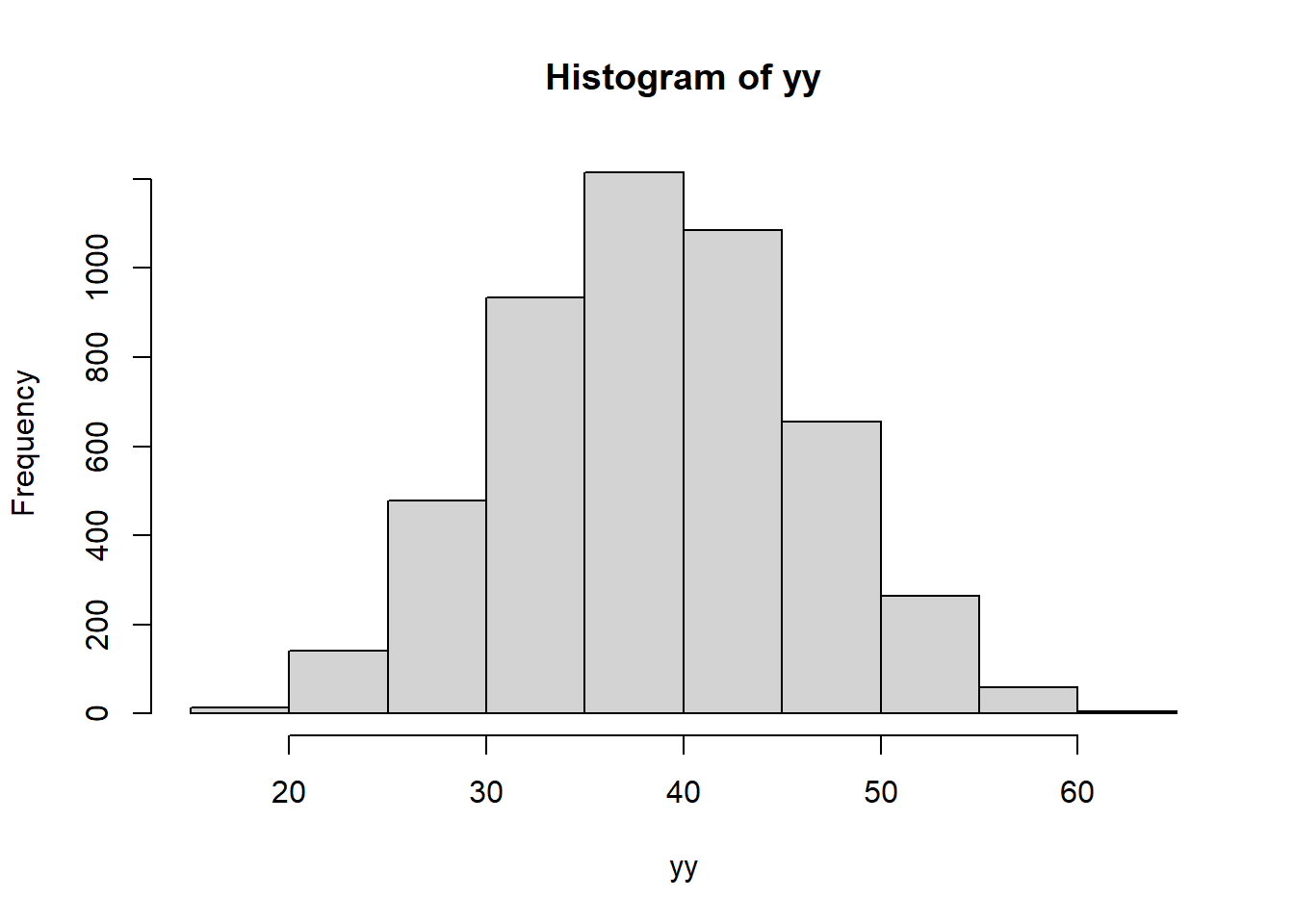

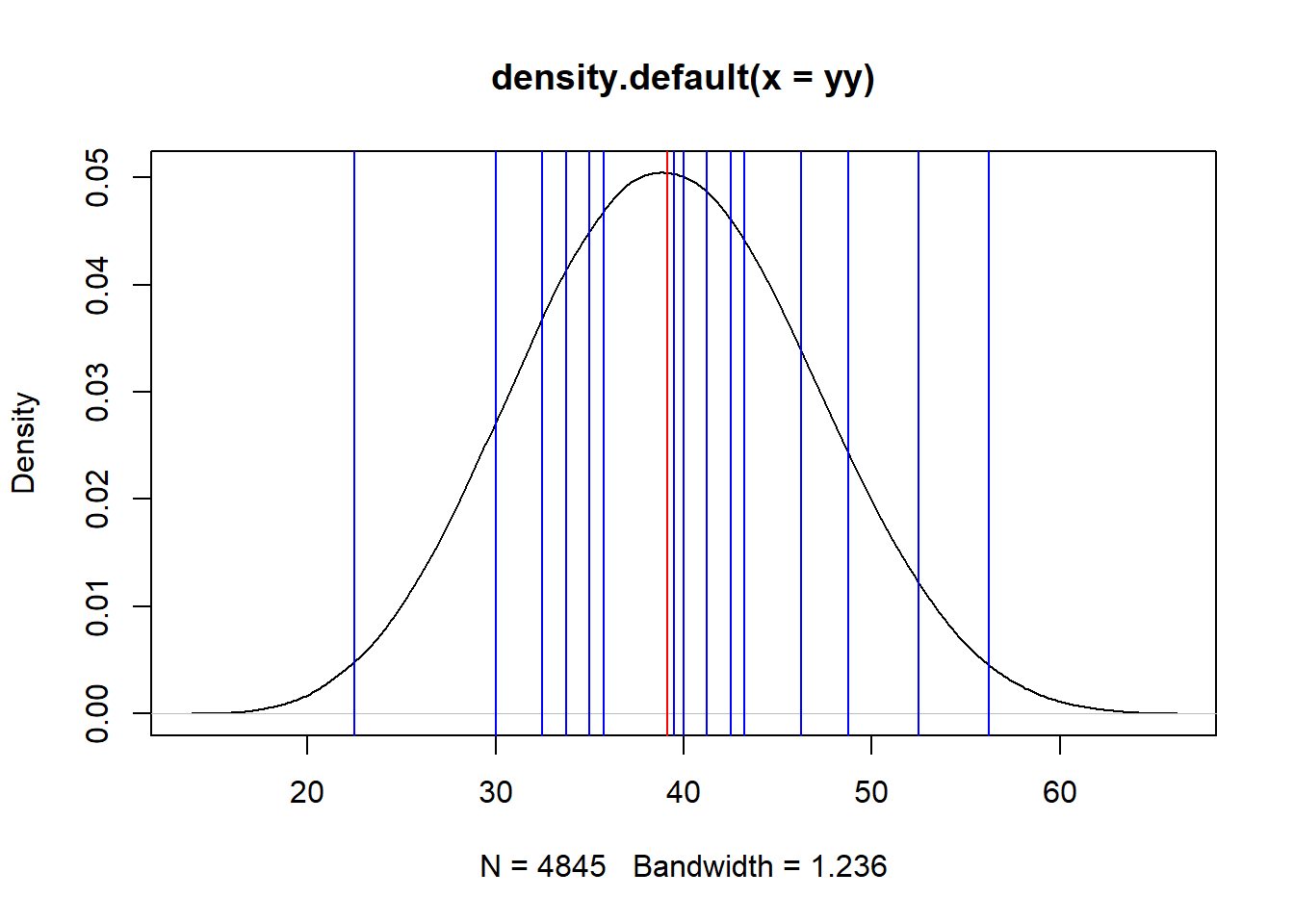
plot(density(yy))
abline(v=39.15,col="red")

for(i in 1:20){
muestra<-sample(y,4)
muestra
mean(muestra)
abline(v=mean(muestra),col="blue")
}

Tarea: Como se obtuvo el valor de 4845. De un población de 30, se obtiene muestras de tamaño 6. ¿Cuántas muestras posibles se pueden obtener?.

4.2 Distribución Normal

Es una distribución de probabilidad que tiene un uso muy importante en diferentes áreas de la estadística y tiene algunas características relevantes:

  • Su centro es el promedio de los datos
  • Su desviación estándar define la forma de la campana, mientras más pequeña la curva se cierre al rededor del promedio y mientras más grande la curva se abre.
  • Es simétrica al rededor del promedio

Para obtener las probabilidades de una distribución normal, se recurre a tablas de la distribución normal o aplicaciones, software estadístico. En general para calcular las probabilidades se trabaja con la distribución normal estándar

Al trabajar con datos de una normal, para obtener las probabilidades se debe estandarizar los datos:

Suponer que: \[X\sim N(\mu=39.15,\sigma=7.5)\] Para estandarizar X, se sigue:

\[Z=\frac{x-\mu}{\sigma}\] Así,

\[Z\sim N(\mu=0,\sigma=1)\]

z<-(yy-mean(yy))/sd(yy)
plot(density(z))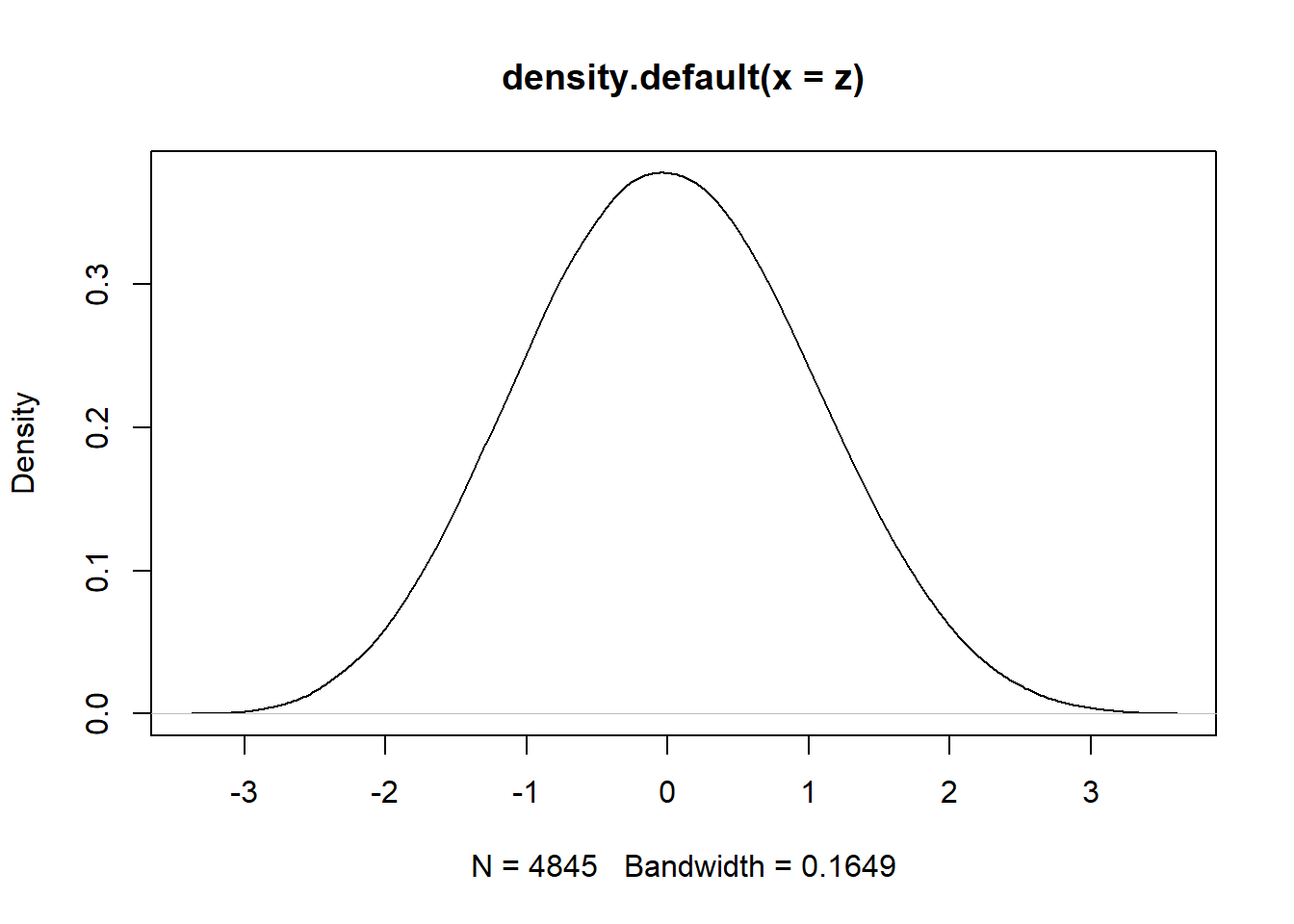

Ejemplo, la estatura de un grupo de personas se distribuye normal con media de 165 cm y un desviación estándar de 10 cm.

¿Cuál sera la probabilidad de que una persona elegida al azar de esta población mida:

  • más de 180
  • menos de 150
  • entre 160 y 170

Solución, sea \(X\) la estatura, esta

\[X\sim N(\mu=165,\sigma=10)\] \[P(X>180)=P\left(\frac{X-\mu}{\sigma}>\frac{180-165}{10}\right)=P(Z>1.5)=1-P(Z<1.5)=\]

\[=1-0.9332=0.0668\]

\[P(X<150)=P(Z<-1.5)=0.0668\] c) entre 160 y 170

\[P(160<X<170)=P(-0.5<Z<0.5)=P(Z<0.5)-P(Z<-0.5)=\] \[=0.6915-0.3085=0.383\]

La tabla calcula las probabilidades del tipo

\[P(Z<z_0)=\phi(z_0)\] \[P(Z>z_0)=1-\phi(z_0)\] \[P(z_0<Z<z_1)=\phi(z_1)-\phi(z_0)\] Ejercicio, de una población de estudiantes de la materia de estadística, donde el promedio de notas final es de 55 puntos con una desviación de 15 puntos. Se toma a un estudiante al azar, cuál es la probabilidad:

  • que el estudiante pase la materia (>50)
  • que el estudiante no pase la materia (<50)
  • que el estudiante tenga una nota superior a 80 puntos
  • que el estudiante tenga una nota menor a 40
  • que el estudiante tenga una nota entre 45 y 50
  • Si el curso tiene 110 estudiantes, ¿cuántos estudiantes se estima que pasaron la materia?

Segundo Parcial: 19 de Agosto.

4.3 Estimación puntual

Cuando hablamos de estimación, nos referimos a una estadística en particular, (no necesariamente al comportamiento de los datos), en todo caso nos interesa el comportamiento de una estadística. Recordar que una estadística es una medida obtenida a partir de una muestra. Las estadísticas que usaremos son:

  • Media o promedio
  • Proporción

En la población de interés la media es:

\[\mu_x=\frac{\sum_{i=1}^N x_i}{N}\]

En la muestra la estimación de este valor es:

\[\bar{X}=\frac{\sum_{i=1}^n x_i}{n}\]

La distribución de la media muestral es de tipo Normal cuando el tamaño de muestra es grande (n>30). Si esto se cumple, podemos afirmar lo siguiente:

\[\bar{X}\sim N\left(\mu=\mu_x,\sigma^2=\frac{\sigma_x^2}{n}\right)\] \[\bar{X}\sim N\left(\mu=\mu_x,\sigma=\frac{\sigma_x}{\sqrt{n}}\right)\]

Donde:

  • \(\mu_x\) es la media poblacional de \(x\)
  • \(\sigma_x^2\) es la varianza poblacional de \(x\)
  • \(\sigma_x\) la desviación estandar \(x\)
  • \(n\) es el tamaño de la muestra

Ejemplo. Se tiene recolectado la media de una muestra de 50 estudiantes de una población, respecto su estatura, el valor es de 164 cm. Se sabe que la varianza de la población es de 81 para la estatura. Calcule:

  • La probabilidad que el promedio de estatura sea mayor a 165
  • La probabilidad que el promedio de estatura sea menor a 160
  • La probabilidad que el promedio de estatura se encuentre entre 162 y 168

Solución, tenemos como información: \[\bar{X}=164\] \[n=50\] \[\sigma_x^2=81\] Ahora, nosotros podemos suponer que:

\[\bar{X}\sim N\left(\mu=164,\sigma=\frac{9}{\sqrt{50}} \right)=N(164,1.27)\]

  • La probabilidad que el promedio de estatura sea mayor a 165

\[P(\bar{X}>165)=P\left(Z>\frac{165-164}{1.27}\right)=P(Z>0.79)=1-\phi(0.79)=\]

\[=1-0.7852=0.2148\]

  • La probabilidad que el promedio de estatura sea menor a 160

\[P(\bar{X}<160)=P(Z<-3.15)=\phi(-3.15)=0.0008\]
* La probabilidad que el promedio de estatura se encuentre entre 162 y 168

\[P(162<\bar{X}<168)=P(-1.57<Z<3.15)=\phi(3.15)-\phi(-1.57)=\]

\[=0.9992-0.0582=0.941\] Un estimador puntual es un único valor obtenido en la muestra. Para las dos estadísticas de interés:

4.3.1 Promedio

Su parámetro

\[\mu_x=\frac{\sum_{i=1}^N x_i}{N}\]

Su estimador

\[\bar{X}=\frac{\sum_{i=1}^n x_i}{n}\]

Donde \(\bar{X}\) es el estimador puntual de \(\mu_x\)

4.3.2 Proporción

El parámetro

\[P_A=\frac{\#A}{N}\] El estimador

\[\hat{P}_a=\frac{\#a}{n}\] Ejemplo, se toma una muestra de 40 personas de una población. En la muestra se identifica a 15 personas que utilizan lentes. ¿Cuál es la estimación de la proporción de personas que usan lentes?

Solución, \(n=40\), \(\#a=15\)

\[\hat{P}_{lentes}=\frac{15}{40}=0.375\]

4.4 Intervalos de confianza

Son estimaciones basadas en intervalos, que además ofrecen un grado de confiabilidad y su ancho depende del error muestral (variabilidad). Los elementos a tener presente al momento de calcular un intervalo de confianza son:

  • Estimador de interés
  • Confiabilidad; usualmente se usa el 95%. Mientras la confiabilidad sea más alta el intervalo de confianza será más amplio
  • El error muestral se lo estima usando la información de la muestra.

4.4.1 Promedio

\(\mu_x\)

\[LI: \bar{X}-Z_{1-\alpha/2}*\frac{\hat{S}_x}{\sqrt{n}}\] \[LS: \bar{X}+Z_{1-\alpha/2}*\frac{\hat{S}_x}{\sqrt{n}}\] Donde \(Z_{1-\alpha/2}\) toma los siguientes valores según el nivel de confiabilidad:

  • 99% de confiabilidad, \(Z=2.56\)
  • 95% de confiabilidad, \(Z=1.96\)
  • 90% de confiabilidad, \(Z=1.64\)

\[\hat{S}_x=\sqrt{\hat{S}^2_x}\]

\[\hat{S}^2_x=\frac{\sum_{i=1}^n (X_i-\bar{X})^2}{n-1}\]

\[\hat{S}^2_x=\frac{\sum_{i=1}^n X_i^2}{n-1}-\frac{n\bar{X}^2}{n-1}\] \[\hat{S}^2_x=\frac{\sum_{i=1}^n X_i^2-n\bar{X}^2 }{n-1}\] Ejercicio, Se tiene una muestra de 20 estudiantes respecto su edad, los datos son: 24, 19, 22, 25, 17, 18, 25, 18, 22, 18, 21, 19, 17, 21, 18, 20, 25, 23, 17, 22.

Se pide calcular el intervalo de confianza al 90%, 95% y 99% de confiabilidad

\[\bar{X}=\frac{\sum_{i=1}^{20}X_i}{20}=\frac{411}{20}=20.55\] \[\hat{S}^2_x=8.05\]

\[\hat{S}_x=\sqrt{8.05}=2.84\]

Al 90%

\[LI:20.55-1.64*\frac{2.84}{\sqrt{20}}=20.55-1.04=19.51\]

\[LS:20.55+1.64*\frac{2.84}{\sqrt{20}}=20.55+1.04=21.59\]

De esta forma el intervalo al 90% es \[[19.51 \quad 21.59]\]

Para el 95%

\[LI:20.55-1.96*\frac{2.84}{\sqrt{20}}=20.55-1.24=19.31\]

\[LS:20.55+1.96*\frac{2.84}{\sqrt{20}}=20.55+1.24=21.79\]

\[[19.31 \quad 21.79]\] ### Proporción

\(P_A:\)

\[LI: \hat{P}_a-Z_{1-\alpha/2}*\sqrt{\frac{\hat{P}_a(1-\hat{P}_a)}{n}}\]

\[LS: \hat{P}_a+Z_{1-\alpha/2}*\sqrt{\frac{\hat{P}_a(1-\hat{P}_a)}{n}}\]

Ejercicio, Se toma una muestra aleatoria de 350 personas de una población. De estas se conoce que 275 personas estudian. Encontrar los intervalos de confianza al 95% y 99% para estimar la proporción de personas que no estudian.

\[\hat{P}_{a}=\frac{\#a}{n}=\frac{75}{350}=0.21\]

Al 95%

\[LI: 0.21-1.96*\sqrt{\frac{0.21(1-0.21)}{350}}=0.21-0.04=0.17\]

\[LS: 0.21+1.96*\sqrt{\frac{0.21(1-0.21)}{350}}=0.21+0.04=0.25\]

\[[0.17 \quad 0.25]\] En porcentaje

\[[17\% \quad 25\%]\]

4.4.2 Porcentaje

\[\hat{P}_a*100=\hat{P}_a\%\]

\[LI: \hat{P}_a\%-Z_{1-\alpha/2}*\sqrt{\frac{\hat{P}_a\%(1-\hat{P}_a\%)}{n}}\]

\[LS: \hat{P}_a\%+Z_{1-\alpha/2}*\sqrt{\frac{\hat{P}_a\%(1-\hat{P}_a\%)}{n}}\]

4.5 Ejercicios

De una población de estudiantes de la materia de estadística, donde el promedio de notas final es de 55 puntos con una desviación de 15 puntos. Se toma a un estudiante al azar, cuál es la probabilidad:

  • que el estudiante tenga una nota entre 45 y 50
  • Si el curso tiene 110 estudiantes, ¿cuántos estudiantes se estima que pasaron la materia?

Solución,

Como información, sea \(X\) la nota de los estudiantes.

\[X\sim N(\mu=55,\sigma=15)\] \[P(45<X<50)=P\left(\frac{45-55}{15}<Z<\frac{50-55}{15}\right)=\]

\[=P(-0.67<Z<-0.33)=\phi(-0.33)-\phi(-0.67)=0.3707-0.2514=0.1193\]

Si el curso tiene 110 estudiantes, ¿cuántos estudiantes se estima que pasaron la materia?

Se debe calcular la probabilidad de pasar la materia \[P(X>50)=P\left(Z>\frac{50-55}{15}\right)=P(Z>-0.33)=1-\phi(-0.33)=\]

\[=1-0.3707=0.63\]

Si el curso tiene 110 estudiantes y la probabilidad de pasar es de \(0.63\), se espera que:

\[110*P(X>50)=110*0.63=69.3\approx 69\]

4.6 Segundo Parcial

Pregunta 1: El área que se encarga de definir el cuestionario a ser usado en un diseño estadístico de recolección es:

Respuesta, es temática

Pregunta 2: Se trata de un tipo de estudio que busca obtener la relación causal entre dos variables:

Respuesta, son los diseños experimentales

Pregunta 3: Son variables que complementan los hallazgos sobre las variables principales:

Respuesta, son las variables de control

Pregunta 4: La pregunta: ¿Cuál es su estado civil? a) Casado/a b) Soltero/a c) Separado/a d) otro, es una pregunta de:

Respuesta, selección única

Pregunta 5: El marco muestral es un listado de la muestra seleccionada

Respuesta, falso ya que el marco muestral es un listado de la población objetivo y este es utilizado para obtener la muestra.

Pregunta 6: Esta técnica de muestreo crea grupos similares al interior con la finalidad de reducir el error muestral

Respuesta, muestreo estratificado

Pregunta 7: Es un muestreo no probabilístico que inicia con una unidad de análisis encontrada y a partir de ella va vinculando las demás unidades de análisis

Respuesta, bola de nieve

Pregunta 8: Se busca definir el tamaño de muestra para hacer una encuesta de intensión de voto para las elecciones de director/a de la carrera de Trabajo Social, se plantea un nivel de confianza del 95%, para un margen de error absoluto del 5%, Definiendo un P máximo, suponiendo que en la carrera existen 2000 estudiantes, se estima que el 10% no responderá la encuesta. Toma DEFF=1.

Respuesta,

\[ n_0=\frac{k^2*N*P*Q}{e^2*(N-1)}=\frac{1.96^2*2000*0.5*0.5}{0.05^2*(2000-1)}=384.3522 \] \[ n_0=\frac{k^2*N*P*Q}{e^2*(N-1)}=\frac{1.96^2*0.5*0.5}{0.05^2}=384.16 \]

\[ n_{1}=\frac{n_0}{1-\frac{n_0}{N}}=\frac{384.3522}{1-\frac{384.3522}{2000}}=475.7871 \] \[ n_{1}=\frac{n_0}{1-\frac{n_0}{N}}=\frac{384.16}{1-\frac{384.16}{2000}}=475.4926 \]

\[ n_{final}=\frac{n_{1}*(Deff)}{(1-\hat{TNR})}=\frac{475.7871*1}{1-0.1}=528.65\approx 529 \] \[ n_{final}=\frac{n_{1}*(Deff)}{(1-\hat{TNR})}=\frac{475.4926*1}{1-0.1}=528.3251\approx 529 \] Suponiendo que no se conoce \(N\)

\[ n_{final}=\frac{n_{0}*(Deff)}{(1-\hat{TNR})}=\frac{384.16*1}{1-0.1}=426.84 \approx 427 \]

Pregunta 9: Se requiere hacer un estudio con una muestra de 770 encuestas en un municipio de Bolivia, se tiene 5 días para el operativo y se sabe que un encuestador puede hacer 6 encuestas diarias. ¿Cuántos encuestadores mínimamente se requieren para cubrir la muestra?

Respuesta, 26

\[\frac{\frac{770}{5}}{6}=25.67\approx 26\] > pregunta 10: Se sabe que la estatura de una población de 500 personas se distribuye de forma normal con media 162 cm y desviación estándar de 9 cm. ¿Cuántas personas se estima que tengan una estatura entre 155 y 165?

Respuesta,

\[P(155<X<165)=P(-0.78<Z<0.33)=\phi(0.33)-\phi(-0.78)=\]

\[=0.6293-0.2177=0.4116\] Finalmente (\(500*0.4116=205.8 \approx 206\)), se espera que 206 personas tenga estaturas entre 155 y 165 en esta población.

Pregunta 11: Se toma una muestra aleatoria de 200 personas de una población. De estas se conoce que 65 personas usan lentes. Encontrar el intervalo de confianza al 95% para estimar la proporción de personas que usan lentes

Respuesta,

\[\hat{P}_{lentes}=\frac{65}{200}=0.325\]

\[LI: 0.325-1.96*\sqrt{\frac{0.325(1-0.325)}{200}}=0.325-0.065=0.26\] \[LS: 0.325+1.96*\sqrt{\frac{0.325(1-0.325)}{200}}=0.325+0.065=0.39\] > Pregunta 12: Se toma una muestra de 15 estudiantes sobre las horas de estudio al día, los datos: 8, 9, 7, 11, 5, 5, 3, 7, 6, 5, 1, 4, 7, 6, 6. Encontrar el intervalo de confianza para el promedio a un nivel de 90% de confiabilidad.

\[\bar{X}=6\]

\[\hat{S}^2_x=\frac{\sum_{i=1}^n X_i^2-n\bar{X}^2 }{n-1}=\frac{622-15*6^2 }{15-1}\]

\[\hat{S}^2_x=5.86\] \[\hat{S}_x=2.42\]

\[LI: 6-1.64*\frac{2.42}{\sqrt{15}}=6-1.025=4.975\]

\[LS: 6+1.64*\frac{2.42}{\sqrt{15}}=6+1.025=7.025\]

Allaire, JJ, Yihui Xie, Jonathan McPherson, Javier Luraschi, Kevin Ushey, Aron Atkins, Hadley Wickham, Joe Cheng, Winston Chang, and Richard Iannone. 2020. Rmarkdown: Dynamic Documents for r. https://CRAN.R-project.org/package=rmarkdown.
R Core Team. 2019. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Xie, Yihui. 2019. Knitr: A General-Purpose Package for Dynamic Report Generation in r. https://CRAN.R-project.org/package=knitr.
———. 2020. Bookdown: Authoring Books and Technical Documents with r Markdown. https://CRAN.R-project.org/package=bookdown.
Xie, Yihui, J. J. Allaire, and Garrett Grolemund. 2018. “How to Read This Book.” Transforming Climate Finance and Green Investment with Blockchains, 1. https://doi.org/10.1016/b978-0-12-814447-3.00041-0.